
已知函數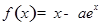
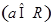 ,
,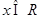 .已知函數
.已知函數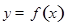 有兩個零點
有兩個零點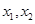 ,且
,且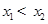 .
.
(1)求 的取值范圍;
的取值范圍;
(2)證明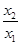 隨著
隨著 的減小而增大;
的減小而增大;
(3)證明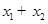 隨著
隨著 的減小而增大.
的減小而增大.
(1)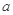 的取值范圍是
的取值范圍是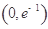 ;(2)詳見試題分析;(3)詳見試題分析.
;(2)詳見試題分析;(3)詳見試題分析.
解析試題分析:(1)先求函數
科目:高中數學
來源:
題型:解答題
科目:高中數學
來源:
題型:解答題
設f(x)是定義在區間(1,+∞)上的函數,其導函數為f′(x).如果存在實數a和函數h(x),其中h(x)對任意的x∈(1,+∞)都有h(x)>0,使得f′(x)=h(x)(x2-ax+1),則稱函數f(x)具有性質P(a).
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區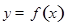 的導數,再分
的導數,再分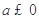 和
和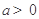 討論
討論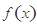 的單調性,將“函數
的單調性,將“函數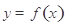 有兩個零點”等價轉化為如下條件同時成立:“1°
有兩個零點”等價轉化為如下條件同時成立:“1°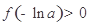 ;2°存在
;2°存在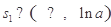 ,滿足
,滿足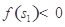 ;3°存在
;3°存在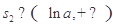 ,滿足
,滿足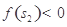 ”,解相應的不等式即可求得
”,解相應的不等式即可求得 的取值范圍;(2)由
的取值范圍;(2)由 分離出參數
分離出參數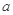 :
: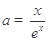 .利用導數討論
.利用導數討論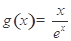 的單調性即可得:
的單調性即可得: 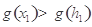 ,從而
,從而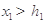 ;類似可得
;類似可得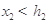 .又由
.又由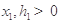 ,得
,得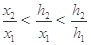 ,最終證得
,最終證得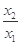 隨著
隨著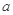 的減小而增大;(3)由
的減小而增大;(3)由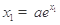 ,
,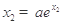 ,可得
,可得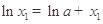 ,
,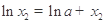 ,作差得
,作差得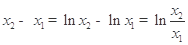 .設
.設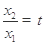 ,則
,則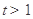 ,且
,且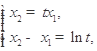 解得
解得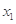 ,
,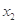 ,可求得
,可求得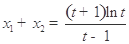 ,構造函數
,構造函數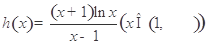 ,利用導數來證明
,利用導數來證明 隨著
隨著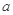 的減小而增大.
的減小而增大.
(1)由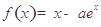 ,可得
,可得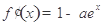 .下面分兩種情況討論:
.下面分兩種情況討論:
(1)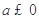 時,
時,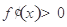 在
在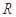 上恒成立,可得
上恒成立,可得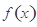 在
在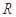 上單調遞增,不合題意.
上單調遞增,不合題意.
(2)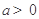 時,由
時,由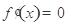 ,得
,得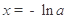 .當
.當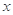 變化時,
變化時,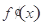 ,
,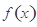 的變化情況如下表:
的變化情況如下表: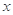
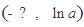
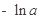
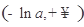
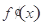
+ 0 - 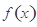
↗ 

習題e百課時訓練系列答案
68所名校圖書小學畢業升學考前突破系列答案
一通百通系統歸類總復習系列答案
新動力系列答案
一路領先大提速同步訓練與測評系列答案
中考導航總復習系列答案
中考快遞同步檢測系列答案
總復習測試系列答案
中教聯中考新突破系列答案
搶分加速度系列答案
 為圓周率,
為圓周率, 為自然對數的底數.
為自然對數的底數.
(1)求函數 的單調區間;
的單調區間;
(2)求 ,
, ,
, ,
, ,
, ,
, 這6個數中的最大數與最小數;
這6個數中的最大數與最小數;
(3)將 ,
, ,
, ,
, ,
, ,
, 這6個數按從小到大的順序排列,并證明你的結論.
這6個數按從小到大的順序排列,并證明你的結論.
(1)設函數f(x)=ln x+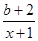 (x>1),其中b為實數.
(x>1),其中b為實數.
①求證:函數f(x)具有性質P(b);
②求函數f(x)的單調區間;
(2)已知函數g(x)具有性質P(2).給定x1,x2∈(1,+∞),x1<x2,設m為實數,α=mx1+(1-m)x2,β=(1-m)x1+mx2,且α>1,β>1,若|g(α)-g(β)|<|g(x1)-g(x2)|,求m的取值范圍.
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號