
設函數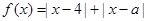
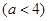
(1)若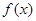 的最小值為3,求
的最小值為3,求 的值;
的值;
(2)求不等式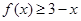 的解集.
的解集.
(1)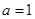 ;(2)
;(2)
解析試題分析:本題考查絕對值不等式的解法和不等式恒成立問題,考查學生的分類討論思想和轉化能力以及計算能力.第一問,利用不等式的性質,得出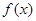 的最小值,列出等式,解出
的最小值,列出等式,解出 的值;第二問,解含參絕對值不等式,用零點分段法去掉絕對值,由于已知中有
的值;第二問,解含參絕對值不等式,用零點分段法去掉絕對值,由于已知中有 和4的大小,所以直接解不等式即可,最后綜合上述所得不等式的解集.
和4的大小,所以直接解不等式即可,最后綜合上述所得不等式的解集.
試題解析:⑴因為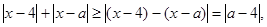
因為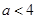 ,所以當且僅當
,所以當且僅當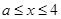 時等號成立,故
時等號成立,故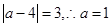 為所求. 4分
為所求. 4分
⑵不等式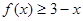 即不等式
即不等式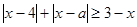
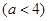 ,
,
①當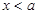 時,原不等式可化為
時,原不等式可化為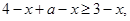
即
所以,當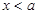 時,原不等式成立.
時,原不等式成立.
②當 時,原不等式可化為
時,原不等式可化為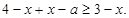
即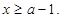 所以,當
所以,當 時,原不等式成立.
時,原不等式成立.
③當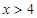 時,原不等式可化為
時,原不等式可化為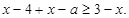
即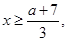 由于
由于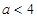 時
時
所以,當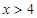 時,原不等式成立.
時,原不等式成立.
綜合①②③可知: 不等式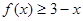 的解集為
的解集為 10分
10分
考點:1.不等式的性質;2.絕對值不等式的解法.


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com