中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

(本題滿(mǎn)分10分)選修4－1：幾何證明選講
如圖，圓O的直徑AB=10，弦DE⊥AB于點(diǎn)H，
AH=2．
(Ⅰ)求DE的長(zhǎng)；
(Ⅱ)延長(zhǎng)ED到P，過(guò)P作圓O的切線(xiàn)，切點(diǎn)為C，
若PC＝2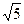，求PD的長(zhǎng)．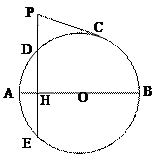

解：(Ⅰ)連接AD，DB，由于AB為圓O的直徑，∴ÐAD^DB．………2分
又AB⊥DE，DH＝HE，
∴DH２＝AH×BH＝2(10－2)＝16，                      …………4分
DH＝4，DE＝8．                                     …………5分
(Ⅱ)PC切圓O于點(diǎn)C，PC２＝PD×PE，                   …………7分
由切割線(xiàn)定理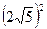＝PD·(PD＋8)，                     …………9分
解得PD＝2．                                         …………10分

解析

練習(xí)冊(cè)系列答案
相關(guān)習(xí)題

科目：高中數(shù)學(xué) 來(lái)源： 題型：解答題

圓O是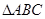的外接圓，過(guò)點(diǎn)C的圓的切線(xiàn)與AB的延長(zhǎng)線(xiàn)交于點(diǎn)D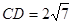，，AB=BC=3，求BD以及AC的長(zhǎng)．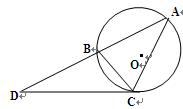

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：解答題

（本小題滿(mǎn)分10分）選修4－1：幾何證明選講
如圖，AB、CD是圓的兩條平行弦，BE//AC，BE交CD于E、交圓于F，過(guò)A點(diǎn)的切線(xiàn)交DC的延長(zhǎng)線(xiàn)于P，PC=ED=1，PA=2．
（I）求AC的長(zhǎng)；
（II）求證：BE＝EF．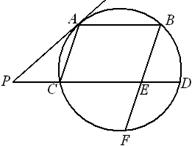

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：解答題

如圖,⊙I是△ABC的內(nèi)切圓.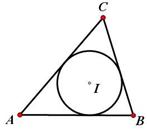

（I）如果∠A=500,求∠BIC的度數(shù)；
（II）若△ABC的周長(zhǎng)為12,面積為6,求⊙I的半徑

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：解答題

．（12分）
如圖，△ABC內(nèi)接于⊙O，過(guò)點(diǎn)A的直線(xiàn)交⊙O于點(diǎn)P，交BC的延長(zhǎng)線(xiàn)于點(diǎn)D，
且AB2＝AP·AD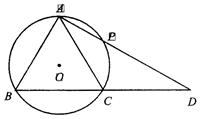

(1)求證：AB＝AC；
(2)如果∠ABC＝60°，⊙O的半徑為1，且P為弧AC的中點(diǎn)，求AD的長(zhǎng)．

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：解答題

(本小題滿(mǎn)分12分) 設(shè)矩形ABCD（AB＞AD）的周長(zhǎng)為12，把它關(guān)于AC折起來(lái)，AB折過(guò)去以后，交CD于點(diǎn)P，求△ADP的面積的最大值及此時(shí)AB邊的長(zhǎng)．
 

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：單選題

曲線(xiàn) （為參數(shù)）與坐標(biāo)軸的交點(diǎn)是（   ）

A．B．C．D．

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：單選題

若直線(xiàn)的參數(shù)方程為，則直線(xiàn)的斜率為（   ）

A．B．C．D．

查看答案和解析>>

科目：高中數(shù)學(xué) 來(lái)源： 題型：解答題

（本試卷共40分，考試時(shí)間30分鐘）
21．（選做題）本大題包括A，B，C，D共4小題，請(qǐng)從這4題中選做2小題． 每小題10分，共20分．請(qǐng)?jiān)诖痤}卡上準(zhǔn)確填涂題目標(biāo)記． 解答時(shí)應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟．
A． 選修4－1：幾何證明選講
如圖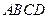，是邊長(zhǎng)為的正方形，以為圓心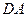，為半徑的圓弧與以為直徑的半⊙O交于點(diǎn)，延長(zhǎng)交于．
（1）求證：是的中點(diǎn)；（2）求線(xiàn)段的長(zhǎng)．

查看答案和解析>>

同步練習(xí)冊(cè)答案