Question

（2013•河西區一模）如圖，在直棱柱ABC-A₁B₁C₁中AB⊥BC，AB=BD=CC₁=2，D為AC的中點．
（I）證明AB₁∥平面BDC₁；
（Ⅱ）證明A₁C⊥平面BDC₁；
（Ⅲ）求二面角A-BC₁-D的正切值．

Answer 1

分析：（I）連接B₁C與BC₁相交于O，連接OD，證明OD∥AB₁，利用線面平行的判定，可得結論；
（Ⅱ）證明BD⊥A₁C，BC₁⊥A₁C，利用線面垂直的判定定理，可證A₁C⊥平面BDC₁；
（Ⅲ）建立空間直角坐標系，求出平面BC₁D的法向量，利用向量的夾角公式，即可求二面角A-BC₁-D的正切值．

解答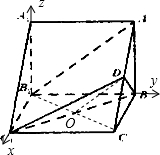：（I）證明：連接B₁C與BC₁相交于O，連接OD
在△CAB₁中，∵O，D分別是B₁C，AC的中點，
∴OD∥AB₁
∵AB₁?平面BDC₁，OD?平面BDC₁，
∴AB₁∥平面BDC₁；
（Ⅱ）證明：直棱柱ABC-A₁B₁C₁中，AA₁⊥平面ABC
∵BD?平面ABC，∴AA₁⊥BD
∵AB=BC=2，D為AC的中點，∴BD⊥AC
∵AA₁∩AC=A，∴BD⊥平面AA₁C₁C
∴BD⊥A₁C①
∵A₁B₁⊥B₁C₁，A₁B₁⊥B₁B，B₁C₁∩B₁B=B
∴A₁B₁⊥平面B₁C₁CB
∴A₁B₁⊥BC₁
在正方形B₁C₁CB中，BC₁⊥B₁C，
∵B₁C，A₁B₁?平面A₁B₁C，B₁C∩A₁B₁=B₁
∴BC₁⊥平面A₁B₁C
∴BC₁⊥A₁C②
由①②，∵BD∩BC₁=B，BD，BC₁?平面BDC₁，
∴A₁C⊥平面BDC₁；
（Ⅲ）解：建立如圖所示的空間直角坐標系，則

CB1

=（-2，-2，0），

BD

=（1，0，1）
設平面BC₁D的法向量

n1

=（x，y，z），則由

n1 • CB1 =0 n1 • BD =0

，可得

-2x-2y=0 x+z=0

，∴可取

n1

=（1，1，-1）
∵平面BC₁A的法向量

n2

=

B1C

=（2，2，0）
設二面角A-BC₁-D的平面角為θ，則cosθ=cos＜

n1

，

n2

＞=

6

3

∴tanθ=

2

2

．

點評：本題考查線面平行，考查線面垂直，考查面面角，考查向量知識的運用，考查學生分析解決問題的能力，屬于中檔題．