
已知 函數
函數
(1)已知任意三次函數的圖像為中心對稱圖形,若本題中的函數 圖像以
圖像以 為對稱中心,求實數
為對稱中心,求實數 和
和 的值
的值
(2)若 ,求函數
,求函數 在閉區間
在閉區間 上的最小值
上的最小值
(1)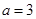 ,
,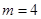 (2)
(2)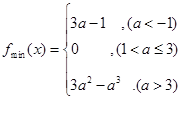
解析試題分析:解:(1)由函數
科目:高中數學
來源:
題型:解答題
已知函數
科目:高中數學
來源:
題型:解答題
已知函數
科目:高中數學
來源:
題型:解答題
設
科目:高中數學
來源:
題型:解答題
已知函數
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區 圖像以
圖像以 為對稱中心,則
為對稱中心,則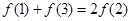 ,代入計算得:
,代入計算得: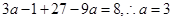 ,故
,故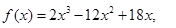
則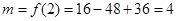
(1)另解:由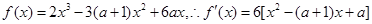
則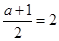 ,則
,則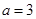 ,故
,故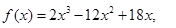
則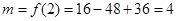
(2)由
因為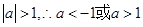 ,討論:
,討論:
1. 若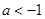 ,如下表:
,如下表:
則此時
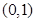
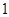
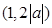
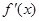
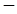
0 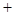

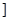

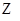
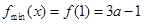
2. 若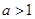 時,如下表:
時,如下表:
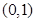
1 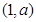
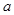
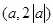


高分裝備復習與測試系列答案
全效學習同步學練測系列答案
高效課堂導學案吉林出版集團有限責任公司系列答案
自我評價與提升系列答案
我為題狂系列答案
快樂練練吧同步練習系列答案
中學生世界系列答案
同步課時練測卷系列答案

口算題卡西安出版社系列答案
 .
.
(1)試問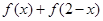 的值是否為定值?若是,求出該定值;若不是,請說明理由;
的值是否為定值?若是,求出該定值;若不是,請說明理由;
(2)定義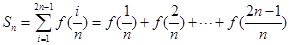 ,其中
,其中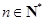 ,求
,求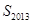 ;
;
(3)在(2)的條件下,令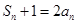 .若不等式
.若不等式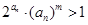 對
對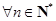 且
且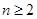 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.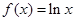 ,
,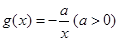
(Ⅰ)當a=1時,若曲線y=f(x)在點M (x0,f(x0))處的切線與曲線y=g(x)在點P (x0, g(x0))處的切線平行,求實數x0的值;
(II)若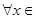 (0,e],都有f(x)≥g(x)+
(0,e],都有f(x)≥g(x)+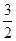 ,求實數a的取值范圍.
,求實數a的取值范圍. , 已知函數
, 已知函數
(Ⅰ) 證明 在區間(-1,1)內單調遞減, 在區間(1, + ∞)內單調遞增;
在區間(-1,1)內單調遞減, 在區間(1, + ∞)內單調遞增;
(Ⅱ) 設曲線 在點
在點 處的切線相互平行, 且
處的切線相互平行, 且 證明
證明 .
.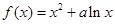 的圖象在點
的圖象在點 處的切線斜率為
處的切線斜率為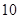 .
.
(Ⅰ)求實數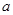 的值;
的值;
(Ⅱ)判斷方程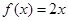 根的個數,證明你的結論;
根的個數,證明你的結論;
(Ⅲ)探究:是否存在這樣的點 ,使得曲線
,使得曲線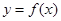 在該點附近的左、右的兩部分分別位于曲線在該點處切線的兩側?若存在,求出點A的坐標;若不存在,說明理由.
在該點附近的左、右的兩部分分別位于曲線在該點處切線的兩側?若存在,求出點A的坐標;若不存在,說明理由.
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號