Question

心理學家發現，學生的接受能力依賴于老師引入概念和描述問題所用的時間，上課開始時，學生的興趣激增，中間有一段不太長的時間，學生的興趣保持較理想的狀態，隨后學生的注意力開始分散，并趨于穩定．分析結果和實驗表明，設提出和講述概念的時間為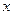（單位：分），學生的接受能力為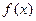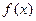（值越大，表示接受能力越強），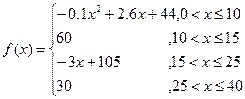
  
（1）開講后多少分鐘，學生的接受能力最強？能維持多少時間？
（2）試比較開講后5分鐘、20分鐘、35分鐘，學生的接受能力的大小；
（3）若一個數學難題，需要56的接受能力以及12分鐘時間，老師能否及時在學生一直達到所需接受能力的狀態下講述完這個難題？

Answer 1

解：(Ⅰ)由題意可知：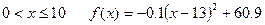
 
所以當X=10時, 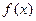的最大值是60,   …………………………………………2分
又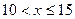, 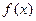="60           "   …………………………………………3分 
所以開講后10分鐘，學生的接受能力最強,并能維持5分鐘. ……………………4分
(Ⅱ）由題意可知: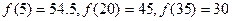 ………………………………5分
所以開講后5分鐘、20分鐘、35分鐘的學生的接受能力從大小依次是
開講后5分鐘、20分鐘、35分鐘的接受能力；………………………………………6分
（Ⅲ）由題意可知：
當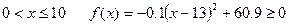          
解得: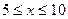                ………………………………………………7分
當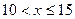 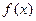=60>56,滿足要求； ………………………………………8分
當,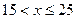
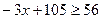
解得: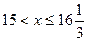               ……………………………………………9分
因此接受能力56及以上的時間是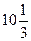分鐘小于12分鐘

解析