
已知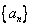 是等差數列,
是等差數列,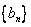 是等比數列,且
是等比數列,且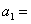
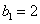 ,
,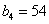 ,又
,又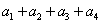
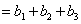 。
。
(1)求數列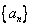 的通項公式和數列
的通項公式和數列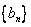 的通項公式;
的通項公式;
(2)設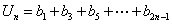 ,其中
,其中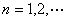 ,求
,求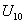 的值。
的值。
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| Sn |
| 1 |
| 4 |
查看答案和解析>>
科目:高中數學 來源:2012年全國普通高等學校招生統一考試文科數學(天津卷解析版) 題型:解答題
已知 是等差數列,其前n項和為
是等差數列,其前n項和為 ,
,  是等比數列,且
是等比數列,且


(I)求數列 與
與 的通項公式;
的通項公式;
(II)記 求證:
求證: ,
, 。
。
【考點定位】本小題主要考查等差數列與等比數列的概念、通項公式、前n項和公式、數列求和等基礎知識.考查化歸與轉化的思想方法.考查運算能力、推理論證能力.
查看答案和解析>>
科目:高中數學 來源:2009-2010學年湖南省株洲市三校聯考高三(上)期中數學試卷(文科)(解析版) 題型:解答題
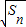 是
是 與(an+1)2的等比中項.
與(an+1)2的等比中項.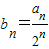 ,數列{bn}的前n項和為Tn,求Tn;
,數列{bn}的前n項和為Tn,求Tn;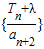 為等比數列?若存在,試求出λ;若不存在,說明理由.
為等比數列?若存在,試求出λ;若不存在,說明理由.查看答案和解析>>
科目:高中數學 來源:2010年江蘇省無錫市江陰市成化高級中學高考數學模擬試卷(05)(解析版) 題型:解答題
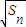 是
是 與(an+1)2的等比中項.
與(an+1)2的等比中項.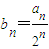 ,數列{bn}的前n項和為Tn,求Tn.
,數列{bn}的前n項和為Tn,求Tn.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com