
 cos2t+
cos2t+ ,試求實數t的取值范圍;
,試求實數t的取值范圍;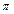 +
+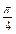 ≤t≤k
≤t≤k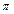 +
+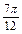 ,k∈Z(2)面積為S=
,k∈Z(2)面積為S=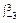 (1-
(1-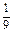 a2)da=4
a2)da=4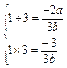
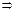
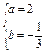 .
. cos2t+
cos2t+ ,
, cos2t+
cos2t+ 對x∈R恒成立,
對x∈R恒成立, cos2t+
cos2t+ ≥1
≥1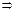 2sin(2t-
2sin(2t-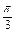 )≥1
)≥1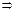 2k
2k +
+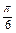 ≤2t-
≤2t-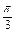 ≤2k
≤2k +
+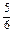
 ,k∈Z
,k∈Z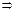 k
k +
+ ≤t≤k
≤t≤k +
+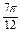 ,k∈Z.
,k∈Z.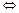 f′(x)≥0恒成立,或者f′(x)≤0恒成立.
f′(x)≥0恒成立,或者f′(x)≤0恒成立.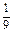 a2.
a2.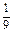 a2與直線b=-1所圍成的封閉圖形,
a2與直線b=-1所圍成的封閉圖形,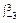 (1-
(1-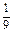 a2)da=4.
a2)da=4.

 特高級教師點撥系列答案
特高級教師點撥系列答案科目:高中數學 來源:不詳 題型:解答題
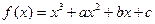 圖像上一點
圖像上一點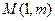 處的切線方程為
處的切線方程為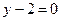 ,其中
,其中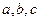 為常數.
為常數. 是否存在單調減區間?若存在,則求出單調減區間(用
是否存在單調減區間?若存在,則求出單調減區間(用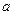 表示);
表示);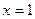 不是函數
不是函數 的極值點,求證:函數
的極值點,求證:函數 的圖像關于點
的圖像關于點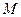 對稱.
對稱.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
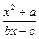 (b,c∈N*),若方程f(x) = x的解為0,2,且f (–2)<–
(b,c∈N*),若方程f(x) = x的解為0,2,且f (–2)<–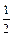 .(Ⅰ)試求函數f(x)的單調區間;(Ⅱ)已知各項不為零的數列{an}滿足4Sn·f (
.(Ⅰ)試求函數f(x)的單調區間;(Ⅱ)已知各項不為零的數列{an}滿足4Sn·f (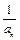 ) = 1,其中Sn為{an}的前n項和.求證:
) = 1,其中Sn為{an}的前n項和.求證: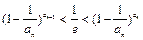 .
.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com