
如圖,半圓O的直徑為2,A為直徑延長(zhǎng)線上的一點(diǎn),OA=2,B為半圓上任意一點(diǎn),以AB為一邊作等邊三角形ABC.問(wèn):點(diǎn)B在什么位置時(shí),四邊形OACB面積最大?
點(diǎn)B在使∠AOB=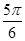 的位置時(shí),四邊形OACB面積最大
的位置時(shí),四邊形OACB面積最大
解析試題分析:在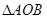 中,由已知OA=2,OB=1,設(shè)∠AOB=
中,由已知OA=2,OB=1,設(shè)∠AOB=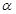 ,則可應(yīng)用余弦定理將AB的長(zhǎng)用
,則可應(yīng)用余弦定理將AB的長(zhǎng)用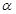 的三角函數(shù)表示出來(lái),進(jìn)而四邊形OACB面積S=S△AOB+S△AB表示成為
的三角函數(shù)表示出來(lái),進(jìn)而四邊形OACB面積S=S△AOB+S△AB表示成為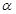 的三角函數(shù),再注意
的三角函數(shù),再注意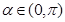 將三角函數(shù)化簡(jiǎn)成為
將三角函數(shù)化簡(jiǎn)成為 的形式,就可求得使四邊形OACB面積最大的角
的形式,就可求得使四邊形OACB面積最大的角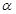 的值,從而就可確定點(diǎn)B的位置.
的值,從而就可確定點(diǎn)B的位置.
試題解析:設(shè)∠AOB=α, .1分
在△AOB中,由余弦定理得
AB2=OA2+OB2-2×OA×OBcos∠AOB
=12+22-2×1×2×cosα
=5-4cosα, .4分
于是,四邊形OACB的面積為
S=S△AOB+S△ABC= OA·OBsinα+
OA·OBsinα+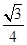 AB2 6分
AB2 6分
= ×2×1×sinα+
×2×1×sinα+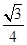 (5-4cosα)
(5-4cosα)
=sinα-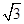 cosα+
cosα+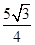
=2sin +
+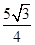 . .10分
. .10分
因?yàn)?<α<π,所以當(dāng)α-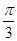 =
=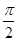 ,α=
,α=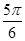 ,
,
即∠AOB=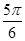 時(shí),四邊形OACB面積最大12分 12分
時(shí),四邊形OACB面積最大12分 12分
考點(diǎn):1.解三角形;2.三角函數(shù)的性質(zhì).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
地面上有兩座塔AB、CD,相距120米,一人分別在兩塔底部測(cè)得一塔頂仰角為另一塔頂仰角的2倍,在兩塔底連線的中點(diǎn)O測(cè)得兩塔頂?shù)难鼋腔橛嘟牵髢勺母叨取?br />
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
在△ABC中,A、B、C所對(duì)的邊分別是a、b、c,bcos B是acos C,ccos A的等差中項(xiàng).
(1)求B的大小;
(2)若 ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
某旅游景點(diǎn)有一座風(fēng)景秀麗的山峰,游客可以乘長(zhǎng)為3km的索道AC上山,也可以沿山路BC上山,山路BC中間有一個(gè)距離山腳B為1km的休息點(diǎn)D.已知∠ABC = 120°,∠ADC = 150°.假設(shè)小王和小李徒步攀登的速度為每小時(shí)1.2km,請(qǐng)問(wèn):兩位登山愛(ài)好者能否在2個(gè)小時(shí)內(nèi)徒步登上山峰(即從B點(diǎn)出發(fā)到達(dá)C點(diǎn)).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
在△ABC中,角A,B, C所對(duì)邊分別為a,b,c,且 .
.
(1)求角A;
(2)若m ,n
,n ,試求|m
,試求|m n|的最小值.
n|的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
在△ABC中,內(nèi)角A,B,C所對(duì)的邊分別為a,b,c,已知sin B(tan A+tan C)=tan Atan C.
(1)求證:a,b,c成等比數(shù)列;
(2)若a=1,c=2,求△ABC的面積S.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
在△ABC中,角A,B,C的對(duì)邊分別為 ,且A,B,C成等差數(shù)列。
,且A,B,C成等差數(shù)列。
(1)若 ,
, ,求△ABC的面積;
,求△ABC的面積;
(2)若 成等比數(shù)列,試判斷△ABC的形狀。
成等比數(shù)列,試判斷△ABC的形狀。
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com