Question

已知復數z₁=i(1-i)³,

(1)求|z₁|;

(2)若|z|=1,求|z-z₁|的最大值.

Answer 1

思路解析:(1)求模應求出復數的實部與虛部再利用|a+bi|=得出;

(2)是考查復數幾何意義的應用.

解:(1)z₁=i(1-i)³=i(-2i)(1-i)=2(1-i),∴|z₁|=.

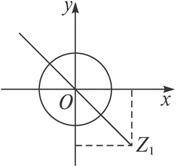
(2)|z|=1可看成半徑為1圓心為(0,0)的圓,而z₁可看成在坐標系中的點(2,-2),

∴|z-z₁|的最大值可以看成點(2,-2)到圓上點距離的最大值,

由圖可知|z-z₁|_max=+1.

變式方法:|z|=1,∴設z=cosθ+isinθ,

|z-z₁|=|cosθ+isinθ-2+2i|=.

當sin(θ-)=-1時,|z-z₁|²取得最大值.

從而得到|z-z₁|的最大值為.

方法歸納  注意此處空半格在設復數的過程中常設為z=a+bi(a、b∈R);在有關的解決軌跡問題中常設z=x+yi從而與解析幾何聯系起來;當復數的模為1時也可以設為z=cosθ+isinθ用三角函數解決相關最值等.