
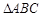 中,角
中,角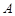 、
、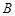 、
、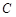 所對的邊分別為
所對的邊分別為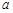 、
、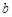 、
、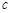 ,滿足
,滿足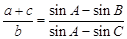 .
.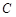 ;
;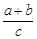 的取值范圍.
的取值范圍. 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
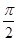 的∠AOB的角平分線上的一點,且OM=1,過M任作一直線與∠AOB的兩邊分別交OA、OB于點E,F(xiàn),記∠OEM=x.
的∠AOB的角平分線上的一點,且OM=1,過M任作一直線與∠AOB的兩邊分別交OA、OB于點E,F(xiàn),記∠OEM=x.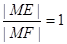 時,試問x的值為多少?(2)求
時,試問x的值為多少?(2)求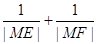 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
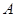 的南偏西
的南偏西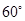 方向的
方向的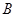 處,且與島嶼
處,且與島嶼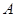 相距12海里,漁船乙以10海里/小時的速度從島嶼
相距12海里,漁船乙以10海里/小時的速度從島嶼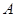 出發(fā)沿正北方向航行,若漁船甲同時從
出發(fā)沿正北方向航行,若漁船甲同時從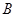 處出發(fā)沿北偏東
處出發(fā)沿北偏東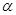 的方向追趕漁船乙,剛好用2小時追上.則
的方向追趕漁船乙,剛好用2小時追上.則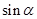 = .
= .
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com