已知
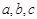
分別是
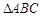
中角
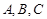
的對邊,且
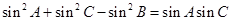
,
⑴求角
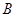
的大小;⑵若
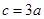
,求
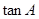
的值.
(1)
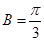
;(2)
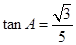
.
試題分析:(1)利用正弦定理的變式
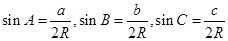
代入原式的兩邊可得邊的關系,再用余弦定理求解即可;(2)利用正弦定理的變式
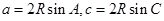
代入
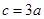
左右兩邊,化為角的關系求解.此兩小題充分考查了正弦定理邊化角,角化邊的功能.
試題解析:(1)由已知條件及正弦定理,得:
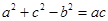
,則
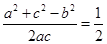
,根據(jù)余弦定理的推論,得
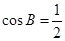
,又
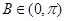
,所以
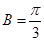
.
(2)因為
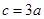
,由正弦定理,得
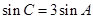
,且
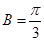
,所以有
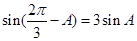
,整理得:
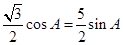
,從而得:
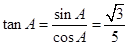
.
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
在
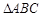
中,角
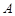
、
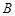
、
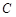
所對的邊分別為
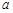
、
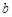
、
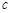
,滿足
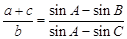
.
(1)求角
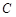
;
(2)求
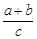
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
下列命題中:①不等式
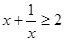
恒成立;②在三角形ABC中,如果有sinA=sinB成立,則必有A=B;③將兩個變量所對應的點在平面直角坐標系中描出來,如果所描的點在散點圖中沒有顯示任何關系則稱變量間是不相關的;④等差數(shù)列{a
n}的首項a
1=-50,公差d=2,前n項和為S
n,則n=25或n=26是使S
n取到最大值;其中為正確命題的序號是:
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
在
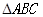
中,角
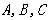
的對邊分別為
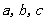
.且
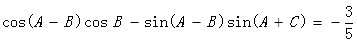
(1)求
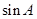
的值;
(2)若

,求向量
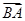
在
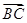
方向上的投影.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
在
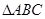
中,角
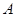
、
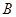
、
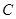
所對的邊分別為
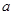
、
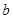
、
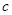
,已知
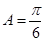
,
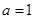
,
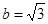
,則
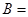
________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
在銳角
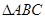
中,角
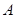
、
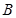
、
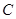
的對邊分別為
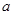
、
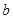
、
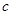
,且
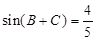
,
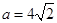
,
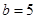
.
(1)求角
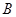
與邊
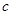
的值;
(2)求向量
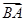
在
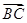
方向上的投影.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
在
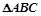
中,角A、B的對邊分別為a、b且A=2B,則
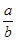
的取值范圍是( )
A.
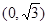
B.
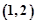
C.
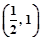
D.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知

中

,則

等于
| A.60° | B.60°或120° | C.30° | D.30°或150° |
查看答案和解析>>

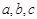 分別是
分別是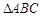 中角
中角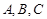 的對邊,且
的對邊,且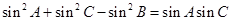 ,
,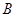 的大小;⑵若
的大小;⑵若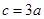 ,求
,求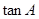 的值.
的值.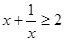 恒成立;②在三角形ABC中,如果有sinA=sinB成立,則必有A=B;③將兩個變量所對應的點在平面直角坐標系中描出來,如果所描的點在散點圖中沒有顯示任何關系則稱變量間是不相關的;④等差數(shù)列{an}的首項a1=-50,公差d=2,前n項和為Sn,則n=25或n=26是使Sn取到最大值;其中為正確命題的序號是: .
恒成立;②在三角形ABC中,如果有sinA=sinB成立,則必有A=B;③將兩個變量所對應的點在平面直角坐標系中描出來,如果所描的點在散點圖中沒有顯示任何關系則稱變量間是不相關的;④等差數(shù)列{an}的首項a1=-50,公差d=2,前n項和為Sn,則n=25或n=26是使Sn取到最大值;其中為正確命題的序號是: .