中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

已知M(-3,0)﹑N(3,0),P為坐標平面上的動點，且直線PM與直線PN的斜率之積為常數(shù)m(m-1,m0).

(1)求P點的軌跡方程并討論軌跡是什么曲線？

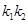(2)若, P點的軌跡為曲線C,過點Q(2,0)斜率為的直線與曲線C交于不同的兩點A﹑B,AB中點為R,直線OR(O為坐標原點)的斜率為，求證為定值；

（3）在（2）的條件下，設(shè)，且，求在y軸上的截距的變化范圍.

 

【答案】

 

(1)略

(2)

【解析】

（2）時，曲線C方程為，設(shè)的方程為：

與曲線C方程聯(lián)立得：，

設(shè)，則①，②，

可得，。

（3）由得代入①②得：

③，④，

③式平方除以④式得：，

而在上單調(diào)遞增，，，

在y軸上的截距為b，=，

 。

 

 

練習冊系列答案
相關(guān)習題

科目：高中數(shù)學 來源： 題型：

下列不等式
①已知a＞0，b＞0，則(a+b)(
1
a
+
1
b
)≥4；
②a2+b2+3＞2a+2b；
③已知m＞0，則
b
a
＜
b+m
a+m
；
④
a-1
+
a+1
＜2
a
(a＞1)．
其中恒成立的是
①②④
①②④
．（把所有成立不等式的序號都填上）

查看答案和解析>>

科目：高中數(shù)學 來源： 題型：

已知M (3, 0)，N (3, 0)，給出曲線：①x y + 5 = 0，②2x + y 12 = 0，③x2 + y2 12x 8y + 51 = 0，④=1. 在所給的曲線上存在點P滿足|MP| = 10 |NP|的所在曲線方程是  __.  

查看答案和解析>>

科目：高中數(shù)學 來源：2013屆山東省濟寧市高二上學期期末考試理科數(shù)學 題型：解答題

(本小題滿分12分)

已知M(-3,0)﹑N(3,0),P為坐標平面上的動點，且直線PM與直線PN的斜率之積為常數(shù)m(m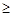-1,m0).

(1)求P點的軌跡方程并討論軌跡是什么曲線？

(2)若, P點的軌跡為曲線C,過點Q(2,0)斜率為的直線與曲線C交于不同的兩點A﹑B,AB中點為R,直線OR(O為坐標原點)的斜率為，求證為定值；

（3）在（2）的條件下，設(shè)，且，求在y軸上的截距的變化范圍.

 

 

 

 

查看答案和解析>>

科目：高中數(shù)學 來源： 題型：

已知M(-3,0),N(3,0),給出下列曲線:①x-y+5=0;

②2x+y-12=0;

③x2+y2-12x-8y+51=0;

④=1.在所給的曲線上存在點P滿足|MP|=10-|NP|的所有曲線方程是___________.

查看答案和解析>>

同步練習冊答案