分析:(1)先求出f′(x)=2ax+b,根據圖象可得f′(x)=2x+1,由此可得a,b的方程組;
(2)由(1)先求出g(x),從而可得g′(x)=
,分
≤1,1<
<2,
≥2三種情況進行討論,根據導數符號與單調性的關系可得最大值;
解答:解:(1)因為f′(x)=2ax+b,由圖可知,f′(x)=2x+1,
由
,解得
,
(2)g(x)=
=
=x+
+1,則g′(x)=1-
=
,
①若
≤1,即0<c≤1時,g′(x)≥0,g(x)在[1,2]上遞增,
故g(x)
max=g(2)=
c+3;
②若1<
<2,即1<c<4,
當1≤x<
時,g′(x)<0,此時g(x)單調遞減;當
<x≤2時,g′(x)>0,此時g(x)單調遞增;
又g(1)=c+2,g(2)=
c+3,
所以當1≤c≤2時,g(1)≤g(2),即g(x)
max=g(2)=
c+3;
當2<x≤4時,g(1)>g(2),即g(x)
max=g(1)=c+2;
③若
≥2,即c≥4時,g′(x)≤0,g(x)在[1,2]上單調遞減,
故g(x)
max=g(1)=c+2;
綜上所述,
g(x)max=;
點評:本題考查利用導數研究函數在閉區間上的最值、函數解析式的求法,考分類討論思想,屬中檔題.

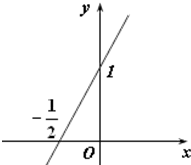 已知二次函數f(x)=ax2+bx+c(c>0)的導函數的圖象如圖所示:
已知二次函數f(x)=ax2+bx+c(c>0)的導函數的圖象如圖所示:

 名校課堂系列答案
名校課堂系列答案