
某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速(km/t)分成六段:


 后得到如圖4的頻率分布直方圖.
后得到如圖4的頻率分布直方圖.
問:(1)求這40輛小型車輛車速的眾數和中位數的估計值.(2)若從車速在 的車輛中任抽取2輛,求抽出的2輛車中車速在
的車輛中任抽取2輛,求抽出的2輛車中車速在 的車輛數
的車輛數 的分布列及其均值(即數學期望).
的分布列及其均值(即數學期望).
(1)眾數的估計值等于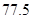 .中位數的估計值為:
.中位數的估計值為: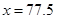 ;
;
(2) 的分布列為:
的分布列為:
均值
0 1 2 
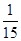
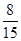
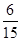
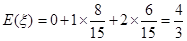 .
.
解析試題分析:(1)眾數的估計值為最高的矩形的中點;如下圖,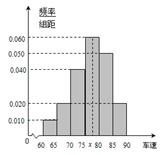
設圖中虛線所對應的車速為 ,若
,若 兩側的矩形的面積相等,則這個
兩側的矩形的面積相等,則這個 就是中位數的估計值;
就是中位數的估計值;
(2)首先看隨機變量可以取哪些值?從圖中可知,這40輛車中,車速在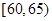 的車輛數為:
的車輛數為: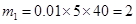 輛,車速在
輛,車速在 的車輛數為:
的車輛數為: 輛.所以
輛.所以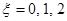 .顯然這是一個超幾何分布,由此可得其分布列及期望.
.顯然這是一個超幾何分布,由此可得其分布列及期望.
試題解析:(1)眾數的估計值為最高的矩形的中點,即眾數的估計值等于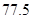 (2分)
(2分)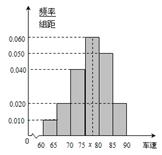
設圖中虛線所對應的車速為 ,則中位數的估計值為:
,則中位數的估計值為: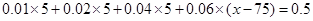 ,解得
,解得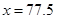
即中位數的估計值為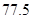 (5分)
(5分)
(2)從圖中可知,車速在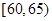 的車輛數為:
的車輛數為: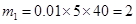 (輛),
(輛),
車速在 的車輛數為:
的車輛數為: (輛) (7分)
(輛) (7分)
∴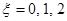 ,
,  ,
,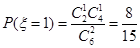 ,
,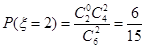 ,
, 的分布列為:
的分布列為:
(10分)
0 1 2 
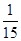
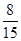
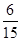
均值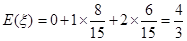 . (12分
. (12分
考點:1、統計基礎知識;2、隨機變量的分布列及期望3、超幾何分布.


 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案科目:高中數學 來源: 題型:解答題
為了了解某年段1000名學生的百米成績情況,隨機抽取了若干學生的百米成績,成績全部介于13秒與18秒之間,將成績按如下方式分成五組:第一組[13,14);第二組[14,15);……;第五組[17,18].按上述分組方法得到的頻率分布直方圖如圖3所示,已知圖中從左到右的前3個組的頻率之比為3∶8∶19,且第二組的頻數為8.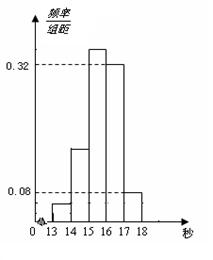
(1)將頻率當作概率,請估計該年段學生中百米成績在[16,17)內的人數;
(2)求調查中隨機抽取了多少個學生的百米成績;
(3)若從第一、五組中隨機取出兩個成績,求這兩個成績的差的絕對值大于1秒的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
由某種設備的使用年限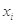 (年)與所支出的維修費
(年)與所支出的維修費 (萬元)的數據資料,算得
(萬元)的數據資料,算得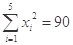 ,
, ,
, ,
,  .
.
(Ⅰ)求所支出的維修費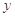 對使用年限
對使用年限 的線性回歸方程
的線性回歸方程 ;
;
(Ⅱ)判斷變量 與
與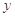 之間是正相關還是負相關;
之間是正相關還是負相關;
(Ⅲ)估計使用年限為8年時,支出的維修費約是多少.
附:在線性回歸方程 中,
中, ,
, ,其中
,其中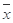 ,
, 為
為
樣本平均值,線性回歸方程也可寫為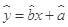 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
2013年9月20日是第25個全國愛牙日。某區衛生部門成立了調查小組,調查 “常吃零食與患齲齒的關系”,對該區六年級800名學生進行檢查,按患齲齒和不患齲齒分類,得匯總數據:不常吃零食且不患齲齒的學生有60名,常吃零食但不患齲齒的學生有100名,不常吃零食但患齲齒的學生有140名.
 | 0.010 | 0.005 | 0.001 |
 | 6.635 | 7.879 | 10.828 |

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某學校900名學生在一次百米測試中,成績全部介于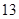 秒與
秒與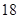 秒之間,抽取其中50個樣本,將測試結果按如下方式分成五組:第一組
秒之間,抽取其中50個樣本,將測試結果按如下方式分成五組:第一組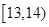 ,第二組
,第二組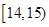 ,…,第五組
,…,第五組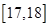 ,下圖是按上述分組方法得到的頻率分布直方圖.
,下圖是按上述分組方法得到的頻率分布直方圖.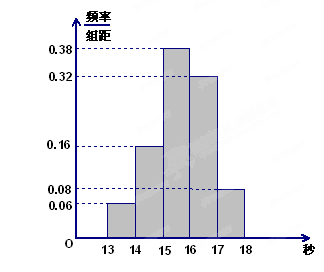
(1)若成績小于14秒認為優秀,求該樣本在這次百米測試中成績優秀的人數;
(2)請估計學校900名學生中,成績屬于第四組的人數;
(3)請根據頻率分布直方圖,求樣本數據的眾數和中位數(保留兩位小數).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了了解某校今年準備報考飛行員的學生的體重情況,將所得的數據整理后,畫出了頻率分布直方圖(如圖所示).已知圖中從左到右的前3個小組的頻率之比為1∶2∶3,第2小組的頻數為12,求抽取的學生人數.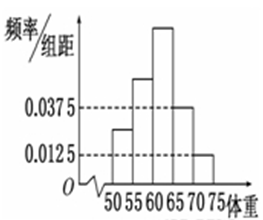
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
2013年4月14日,CCTV財經頻道報道了某地建筑市場存在違規使用未經淡化海砂的現象.為了研究使用淡化海砂與混凝土耐久性是否達標有關,某大學實驗室隨機抽取了60個樣本,得到了相關數據如下表:
| | 混凝土耐久性達標 | 混凝土耐久性不達標 | 總計 |
| 使用淡化海砂 | 25 |  | 30 |
| 使用未經淡化海砂 | 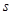 | 15 | 30 |
| 總計 | 40 | 20 | 60 |
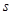 ,
, 的值,利用獨立性檢驗的方法判斷,能否在犯錯誤的概率不超過1%的前提下,認為使用淡化海砂與混凝土耐久性是否達標有關?
的值,利用獨立性檢驗的方法判斷,能否在犯錯誤的概率不超過1%的前提下,認為使用淡化海砂與混凝土耐久性是否達標有關?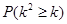 | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
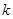 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在每年的春節后,某市政府都會發動公務員參與到植樹活動中去.為保證樹苗的質量,該市林管部門在植樹前,都會在植樹前對樹苗進行檢測.現從甲乙兩種樹苗中各抽測了10株樹苗的高度,量出樹苗的高度如下(單位:厘米):
甲:
乙: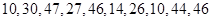
(1)根據抽測結果,完成答題卷中的莖葉圖,并根據你填寫的莖葉圖,對甲、乙兩種樹苗的高度作比較,寫出兩個統計結論;
(2)設抽測的10株甲種樹苗高度平均值為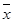 ,將這10株樹苗的高度依次輸入按程序框圖進行的運算,問輸出的
,將這10株樹苗的高度依次輸入按程序框圖進行的運算,問輸出的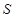 大小為多少?并說明
大小為多少?并說明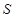 的統計學意義.
的統計學意義.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某數學老師對本校2013屆高三學生某次聯考的數學成績進行分析,按1:50進行分層抽樣抽取的20名學生的成績進行分析,分數用莖葉圖記錄如下: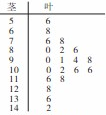
得到頻率分步表如下:
(1)求表中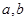 的值,并估計這次考試全校學生數學成績及格率(分數在
的值,并估計這次考試全校學生數學成績及格率(分數在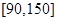 范圍為及格);
范圍為及格);
(2)從大于等于110分的學生中隨機選2名學生得分,求2名學生的平均得分大于等于130分的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com