
在△ABC中,角A,B,C所對(duì)的邊分別為a,b,c且滿足c sinA="a" cosC.
(1)求角C的大小;
(2)求 sinA –cos(B+C)的取值范圍.
sinA –cos(B+C)的取值范圍.
(1)C= ;(2)
;(2)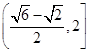
解析試題分析:(1)由正弦定理得sinCsinA="sinAcosC" , 所以tanC=1,則C=
(2) sinA –cos(B+C)=
sinA –cos(B+C)=  sinA –cos(
sinA –cos(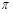 -A )
-A )
= sinA –cosA=2sin(A+
sinA –cosA=2sin(A+ )
)
又 0 < A< 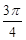 ,
,  < A+
< A+ <
< 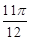 ,
,
所以 sinA –cos(B+C) 的取值范圍
sinA –cos(B+C) 的取值范圍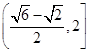
試題解析:(1)已知c sinA="a" cosC
由正弦定理得sinCsinA="sinAcosC" ,
因?yàn)?<A<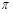 , 所以sinA>0, 得sinC="cosC" ,
, 所以sinA>0, 得sinC="cosC" ,
又cosC ≠0,所以tanC=1,則C=
(2)已知A+B+C=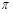 ,所以
,所以 sinA –cos(B+C)=
sinA –cos(B+C)=  sinA –cos(
sinA –cos(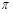 -A ) =
-A ) = sinA –cosA=2sin(A+
sinA –cosA=2sin(A+ )
)
又C= ,所以0 < A<
,所以0 < A< 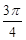 ,
,  < A+
< A+ <
< 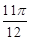 ,
,
所以sin(A+ )
)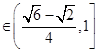 ,
,
所以2sin(A+ )
)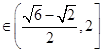
綜上所述, sinA –cos(B+C) 的取值范圍
sinA –cos(B+C) 的取值范圍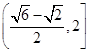
考點(diǎn):正弦定理,三角函數(shù)恒等變換.


 應(yīng)用題天天練四川大學(xué)出版社系列答案
應(yīng)用題天天練四川大學(xué)出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
設(shè) 的內(nèi)角
的內(nèi)角 所對(duì)的邊為
所對(duì)的邊為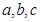 ;則下列命題正確的是
;則下列命題正確的是
①若 ;則
;則
②若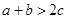 ;則
;則
③若 ;則
;則
④若 ;則
;則
⑤若 ;則
;則
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
設(shè)△ABC的內(nèi)角A、B、C所對(duì)的邊分別為a、b、c,且 .
.
(1)求角A的大小; (2)若 ,求△ABC的周長(zhǎng)L的取值范圍.
,求△ABC的周長(zhǎng)L的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
設(shè)銳角三角形ABC的內(nèi)角A、B、C的對(duì)邊分別為 .
.
(1)求角B的大小;
(2)若a=3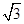 ,c=5,求b.
,c=5,求b.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
某艦艇在A處測(cè)得遇險(xiǎn)漁船在北偏東 距離為10海里的C處,此時(shí)得知,該漁船沿北偏東
距離為10海里的C處,此時(shí)得知,該漁船沿北偏東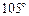 方向,以每小時(shí)9海里的速度向一小島靠近,艦艇時(shí)速21海里,則艦艇到達(dá)漁船的最短時(shí)間是___________.
方向,以每小時(shí)9海里的速度向一小島靠近,艦艇時(shí)速21海里,則艦艇到達(dá)漁船的最短時(shí)間是___________.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com