
定義在 上的可導(dǎo)函數(shù)
上的可導(dǎo)函數(shù)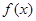 ,當(dāng)
,當(dāng)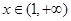 時(shí),
時(shí),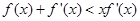 恒成立,
恒成立, ,則
,則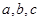 的大小關(guān)系為 ( )
的大小關(guān)系為 ( )
A.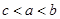 B.
B.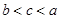 C.
C.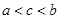 D.
D.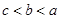
A
【解析】
試題分析:當(dāng)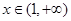 時(shí),
時(shí),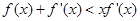 恒成立知,當(dāng)
恒成立知,當(dāng)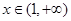 時(shí), ,所以
時(shí), ,所以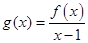 在
在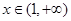 上是增函數(shù).因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013090413072456436364/SYS201309041307400018454719_DA.files/image004.png">
上是增函數(shù).因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013090413072456436364/SYS201309041307400018454719_DA.files/image004.png">
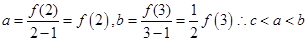 。故選A。
。故選A。
考點(diǎn):函數(shù)的單調(diào)性
點(diǎn)評:對于比較復(fù)雜的函數(shù),求其單調(diào)性常用到導(dǎo)數(shù),在求解過程中要用到的結(jié)論是:
 為增函數(shù);
為增函數(shù);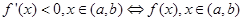 為減函數(shù)。
為減函數(shù)。


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:2010-2011年遼寧省高二下學(xué)期期末考試數(shù)學(xué)理科 題型:解答題
(本小題滿分12分)(1)對于定義在 上的函數(shù)
上的函數(shù) ,滿足
,滿足 ,求證:函數(shù)
,求證:函數(shù) 在
在 上是減函數(shù);
上是減函數(shù);
(2)請你認(rèn)真研讀(1)中命題并聯(lián)系以下命題:若 是定義在
是定義在 上的可導(dǎo)函數(shù),滿足
上的可導(dǎo)函數(shù),滿足 ,則
,則 是
是 上的減函數(shù)。然后填空建立一個(gè)普遍化的命題
上的減函數(shù)。然后填空建立一個(gè)普遍化的命題 :
:
設(shè) 是定義在
是定義在 上的可導(dǎo)函數(shù),
上的可導(dǎo)函數(shù), ,若
,若  +
+
 ,
,
則 是 上的減函數(shù)。
上的減函數(shù)。
注:命題的普遍化就是從考慮一個(gè)對象過渡到考慮包含該對象的一個(gè)集合;或者從考慮一個(gè)較小的集合過渡到考慮包含該較小集合的更大集合。
(3)證明(2)中建立的普遍化命題。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013-2014學(xué)年山東省萊蕪市高三上學(xué)期期末考試?yán)砜茢?shù)學(xué)試卷(解析版) 題型:選擇題
已知定義在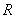 上的可導(dǎo)函數(shù)
上的可導(dǎo)函數(shù)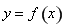 的導(dǎo)函數(shù)為
的導(dǎo)函數(shù)為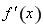 ,滿足
,滿足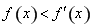 ,且
,且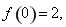 則不等式
則不等式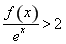 的解集為( )
的解集為( )
A. 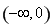 B.
B.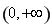 C.
C.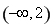 D.
D.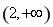
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014屆河南省高二上學(xué)期期末考試文科數(shù)學(xué)試卷(解析版) 題型:選擇題
已知: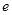 是自然對數(shù)的底數(shù),
是自然對數(shù)的底數(shù),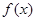 為定義在
為定義在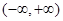 上的可導(dǎo)函數(shù),且
上的可導(dǎo)函數(shù),且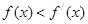 對于
對于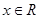 恒成立,則( )
恒成立,則( )
A.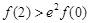 ,
,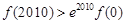 B.
B.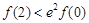 ,
,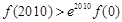
C.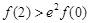 ,
,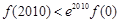 D.
D.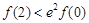 ,
,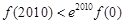
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013屆全國100所名校高三學(xué)期初理科數(shù)學(xué)示范卷(解析版) 題型:選擇題
已知 為定義在
為定義在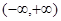 上的可導(dǎo)函數(shù),且
上的可導(dǎo)函數(shù),且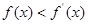 對于任意
對于任意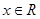 恒成立,則( )
恒成立,則( )
A. 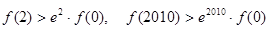
B. 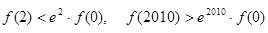
C. 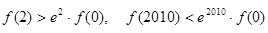
D. 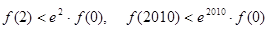
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年安徽省高三上學(xué)期期末考試?yán)砜茢?shù)學(xué) 題型:填空題
已知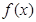 為定義在
為定義在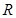 上的可導(dǎo)函數(shù),且
上的可導(dǎo)函數(shù),且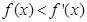 對于
對于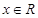 恒成立且e為自然對數(shù)的底,則
恒成立且e為自然對數(shù)的底,則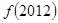 與
與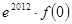 的大小關(guān)系是
的大小關(guān)系是
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com