
�^���タC��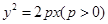 �ϵ��c(di��n)M�քe��C�Ĝ�(zh��n)����x�S���������ɗl������C�Ĝ�(zh��n)����x�S����߅�L��4�������Σ��c(di��n)M�ڵ�һ����.
�ϵ��c(di��n)M�քe��C�Ĝ�(zh��n)����x�S���������ɗl������C�Ĝ�(zh��n)����x�S����߅�L��4�������Σ��c(di��n)M�ڵ�һ����.
��1�����タC�ķ��̼��c(di��n)M������(bi��o)��
��2���^�c(di��n)M���Aб�ǻ��a(b��)�ăɗlֱ���քe�c���タC����A��B���c(di��n)����ֱ��AB�^�c(di��n)��0��-1������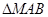 ����e.
����e.
��1��y2��8x��(2��4)����2��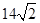 .
.
����ԇ�}���������}��Ҫ���钁�タ�Ę�(bi��o)��(zh��n)���̼�������|(zh��)���f�_(d��)�������c(di��n)��ֱ���ľ��x����������e��ʽ�Ȼ��A(ch��)֪�R������W(xu��)���ķ������}��Q���}���������D(zhu��n)��������Ӌ(j��)������.��һ�������}��Y(ji��)�ϒ��タ�D��õ�M�c(di��n)����(bi��o)�����뒁�タ�����У����P��ֵ���Ķ��õ����タ�Ę�(bi��o)��(zh��n)���̼�M�c(di��n)����(bi��o)���ڶ������O(sh��)��A��B�c(di��n)����(bi��o)������M�c(di��n)���քe�õ�ֱ��MA��ֱ��MB��б�ʣ���?y��n)��ֱ���Aб�ǻ��a(b��)�����ԃ�ֱ����б����Ӟ�0�������õ�y(t��ng)1��y2����8�����뵽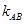 �еõ�ֱ��AB��б�ʣ����ǵõ�ֱ��AB�ķ��̣���ֱ���c���タ(li��n)�����õ�
�еõ�ֱ��AB��б�ʣ����ǵõ�ֱ��AB�ķ��̣���ֱ���c���タ(li��n)�����õ�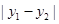 ����
����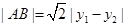 ��
��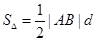 ����
����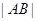 �Ã��c(di��n)�g���x��ʽ�D(zhu��n)����d��M��ֱ��AB�ľ��x���Ķ��õ�
�Ã��c(di��n)�g���x��ʽ�D(zhu��n)����d��M��ֱ��AB�ľ��x���Ķ��õ�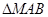 ����e.
����e.
��1�����タC�Ĝ�(zh��n)��x����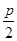 �����}��M(4��
�����}��M(4��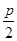 ��4)��
��4)��
�t42��2p(4��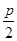 )�����p��4��
)�����p��4��
�ʒ��タC�ķ��̞�y2��8x���c(di��n)M������(bi��o)��(2��4)�� 3��
��2���O(sh��)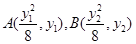 ��
��
ֱ��MA��б��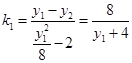 ��ͬ��ֱ��MB��б��
��ͬ��ֱ��MB��б��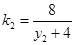 ��
��
���}�O(sh��)��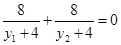 ��������y1��y2����8��
��������y1��y2����8��
ֱ��AB��б��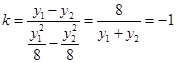 �� 6��
�� 6��
����ֱ��AB�ķ��̞�y����x��1��
��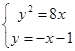 ��y2��8y��8��0��
��y2��8y��8��0��
|y1��y2|��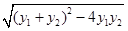 ��
�� ��
��
����|AB|��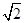 |y1��y2|��8�� 10��
|y1��y2|��8�� 10��
�c(di��n)M��ֱ��AB�ľ��x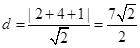 ��
��
�t��MAB����eS��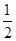 |AB|��d��
|AB|��d��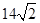 �� 12��
�� 12��
���c(di��n)�����タ�Ę�(bi��o)��(zh��n)���̼�������|(zh��)���f�_(d��)�������c(di��n)��ֱ���ľ��x����������e��ʽ.


 �����W(xu��)���A�����ϵ�д�
�����W(xu��)���A�����ϵ�д� �W(xu��)����܇���옷����������I(y��)�½����������ϵ�д�
�W(xu��)����܇���옷����������I(y��)�½����������ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
(��С�}�M��12�֣�
��֪�c(di��n)A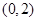 ,�E�AE:
,�E�AE: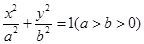 ���x���ʞ�
���x���ʞ�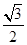 ��F�ǙE�AE���ҽ��c(di��n)��ֱ��AF��б�ʞ�
��F�ǙE�AE���ҽ��c(di��n)��ֱ��AF��б�ʞ�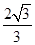 ��O������(bi��o)ԭ�c(di��n)
��O������(bi��o)ԭ�c(di��n)
��I����E�ķ��̣�
��II���O(sh��)�^�c(di��n)A�Ą�(d��ng)ֱ�� �cE �ཻ��P,Q���c(di��n)����(d��ng)
�cE �ཻ��P,Q���c(di��n)����(d��ng)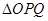 ����e���r(sh��)����
����e���r(sh��)���� ��ֱ������.
��ֱ������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�O(sh��)���タ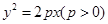 �Ľ��c(di��n)��
�Ľ��c(di��n)��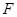 ���c(di��n)
���c(di��n) ������
������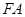 �����c(di��n)�ڒ��タ�ϣ��O(sh��)��(d��ng)ֱ��
�����c(di��n)�ڒ��タ�ϣ��O(sh��)��(d��ng)ֱ��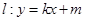 �c���タ�������c(di��n)
�c���タ�������c(di��n)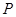 �����c���タ�Ĝ�(zh��n)���ཻ���c(di��n)
�����c���タ�Ĝ�(zh��n)���ཻ���c(di��n)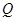 ����
����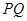 ��ֱ���ĈAӛ��A
��ֱ���ĈAӛ��A ��
��
��1����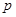 ��ֵ��
��ֵ��
��2���C�����A �c
�c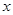 �S������c(di��n)��
�S������c(di��n)��
��3��������(bi��o)ƽ�����Ƿ���ڶ��c(di��n)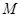 ��ʹ�ÈA
��ʹ�ÈA ���^�c(di��n)
���^�c(di��n)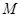 �������ڣ����
�������ڣ����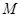 ������(bi��o)���������ڣ��f�����ɣ�
������(bi��o)���������ڣ��f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�E�A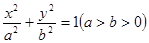 ���ҽ��c(di��n)��
���ҽ��c(di��n)��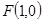 ,�x����
,�x����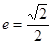 ,
,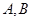 �ǙE�A�ϵĄ�(d��ng)�c(di��n)��
�ǙE�A�ϵĄ�(d��ng)�c(di��n)��
��1����E�A��(bi��o)��(zh��n)���̣�
��2����ֱ��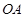 �c
�c ��б�ʳ˷e
��б�ʳ˷e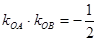 ,��(d��ng)�c(di��n)
,��(d��ng)�c(di��n) �M��
�M�� ,�����Ќ�(sh��)��(sh��)
,�����Ќ�(sh��)��(sh��)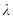 �鳣��(sh��)�������Ƿ���ڃɂ�(g��)���c(di��n)
�鳣��(sh��)�������Ƿ���ڃɂ�(g��)���c(di��n)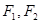 ,ʹ��
,ʹ��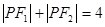 ��������,��
��������,��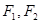 ������(bi��o)��
������(bi��o)��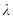 ��ֵ����������,�f�����ɣ�
��ֵ����������,�f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��13�֣���2011•����O(sh��)�E�A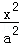 +
+ =1��a��b��0�������ҽ��c(di��n)�քe��F1��F(xi��n)2���c(di��n)P��a��b���M��|PF2|=|F1F2|��
=1��a��b��0�������ҽ��c(di��n)�քe��F1��F(xi��n)2���c(di��n)P��a��b���M��|PF2|=|F1F2|��
������E�A���x����e��
�����O(sh��)ֱ��PF2�c�E�A�ཻ��A��B���c(di��n)����ֱ��PF2�c�A��x+1��2+ =16�ཻ��M��N���c(di��n)����|MN|=
=16�ཻ��M��N���c(di��n)����|MN|= |AB|����E�A�ķ��̣�
|AB|����E�A�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�E�A ��һ��(g��)���c(di��n)��
��һ��(g��)���c(di��n)��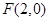 �����x���ʞ�
�����x���ʞ�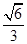 ��
��
��1����E�A���̣�
��2���^�c(di��n)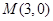 ��б�ʞ�
��б�ʞ�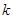 ��ֱ���c�E�A����
��ֱ���c�E�A���� ���c(di��n)���c(di��n)
���c(di��n)���c(di��n) �P(gu��n)��
�P(gu��n)�� �S���Q�c(di��n)��
�S���Q�c(di��n)��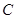 �����
�����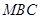 ��e�����ֵ.
��e�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�E�A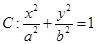
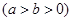 ���x���ʞ�
���x���ʞ�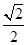 ����ԭ�c(di��n)��A�ģ��E�A�Ķ̰��S�L��돽�ĈA�cֱ��
����ԭ�c(di��n)��A�ģ��E�A�Ķ̰��S�L��돽�ĈA�cֱ��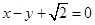 ���У�
����
��1����E�A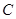 �ķ��̣�
�ķ��̣�
��2�����^�c(di��n)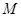 (2��0)��ֱ���c�E�A
(2��0)��ֱ���c�E�A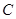 �ཻ�ڃ��c(di��n)
�ཻ�ڃ��c(di��n)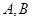 ���O(sh��)
���O(sh��)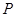 ��E�A��һ�c(di��n)���ҝM��
��E�A��һ�c(di��n)���ҝM��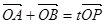 ��
��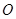 ������(bi��o)ԭ�c(di��n)������(d��ng)
������(bi��o)ԭ�c(di��n)������(d��ng)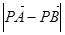 ��
��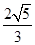 �r(sh��)����(sh��)��(sh��)
�r(sh��)����(sh��)��(sh��)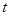 ȡֵ������
ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�E�A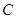 ��������ԭ�c(di��n)
��������ԭ�c(di��n)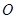 �����c(di��n)��
�����c(di��n)�� �S�ϣ��x���ʞ�
�S�ϣ��x���ʞ� ���ҽ��c(di��n)������c(di��n)�ľ��x��
���ҽ��c(di��n)������c(di��n)�ľ��x��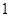 .
.
������E�A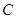 �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
������ֱ��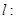
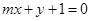 �c�E�A
�c�E�A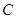 ����
���� ���c(di��n)���Ƿ���ڌ�(sh��)��(sh��)
���c(di��n)���Ƿ���ڌ�(sh��)��(sh��) ��ʹ
��ʹ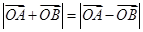 �����������ڣ���
�����������ڣ��� ��ֵ���������ڣ�Ո�f������.
��ֵ���������ڣ�Ո�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�E�A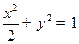 ��
�� ������(bi��o)ԭ�c(di��n)���E�A���Ҝ�(zh��n)���c
������(bi��o)ԭ�c(di��n)���E�A���Ҝ�(zh��n)���c �S�Ľ��c(di��n)��
�S�Ľ��c(di��n)�� ��
��
��1���c(di��n)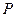 ����֪�E�A�ϣ���(d��ng)�c(di��n)
����֪�E�A�ϣ���(d��ng)�c(di��n)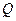 �M��
�M��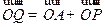 �����(d��ng)�c(di��n)
�����(d��ng)�c(di��n)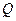 ��܉�E���̣�
��܉�E���̣�
��2���^�E�A�ҽ��c(di��n) ��ֱ���c�E�A�����c(di��n)
��ֱ���c�E�A�����c(di��n)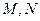 ����
����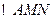 ����e�����ֵ
����e�����ֵ
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com