
設函數f(x)=lnx﹣ax,a∈R.
(1)當x=1時,函數f(x)取得極值,求a的值;
(2)當a>0時,求函數f(x)在區間[1,2]的最大值;
(3)當a=﹣1時,關于x的方程2mf(x)=x2(m>0)有唯一實數解,求實數m的值.
解:(1)f(x)的定義域為(0,+∞),所以f′(x)=![]() ﹣a=
﹣a=![]() .
.
因為當x=1時,函數f(x)取得極值,所以f′(1)=1﹣a=0,所以a=1.
經檢驗,a=1符合題意.(不檢驗不扣分)
(2)f′(x)=![]() ﹣a=
﹣a=![]() ,x>0.
,x>0.
令f′(x)=0得x=![]() .因為x∈(0,
.因為x∈(0,![]() )時,f′(x)>0,x∈(
)時,f′(x)>0,x∈(![]() ,+∞)時,f′(x)<0,
,+∞)時,f′(x)<0,
所以f(x)在(0,![]() )遞增,在(
)遞增,在(![]() ,+∞)遞減,
,+∞)遞減,
①當0<![]() ≤1,即a≥1時,f(x)在(1,2)上遞減,所以x=1時,f(x)取最大值f(1)=﹣a;
≤1,即a≥1時,f(x)在(1,2)上遞減,所以x=1時,f(x)取最大值f(1)=﹣a;
②當1<![]() <2,即
<2,即![]() <a<1時,f(x)在(1,
<a<1時,f(x)在(1,![]() )上遞增,在(
)上遞增,在( ![]() ,2)上遞減,
,2)上遞減,
所以x=![]() 時,f(x)取最大值f(
時,f(x)取最大值f(![]() )=﹣lna﹣1;
)=﹣lna﹣1;
③當![]() ≥2,即0<a≤
≥2,即0<a≤![]() 時,f(x)在(1,2)上遞增,所以x=2時,f(x)取最大值f(2)=ln2﹣2a.
時,f(x)在(1,2)上遞增,所以x=2時,f(x)取最大值f(2)=ln2﹣2a.
綜上,①當0<a≤![]() 時,f(x)最大值為ln2﹣2a;②當
時,f(x)最大值為ln2﹣2a;②當![]() <a<1時,f(x)最大值為﹣lna﹣1;
<a<1時,f(x)最大值為﹣lna﹣1;
③當a≥1時,f(x)最大值為﹣a.
(3)因為方程2mf(x)=x2有唯一實數解,
所以x2﹣2mlnx﹣2mx=0有唯一實數解,
設g(x)=x2﹣2mlnx﹣2mx,
則g′(x)=![]() ,令g′(x)=0,x2﹣mx﹣m=0.
,令g′(x)=0,x2﹣mx﹣m=0.
因為m>0,x>0,所以x1=![]() <0(舍去),x2=
<0(舍去),x2=![]() ,
,
當x∈(0,x2)時,g′(x)<0,g(x)在(0,x2)上單調遞減,
當x∈(x2,+∞)時,g′(x)>0,g(x)在(x2,+∞)單調遞增,
當x=x2時,g(x)取最小值g(x2).
則![]()
即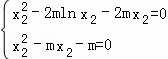
所以2mlnx2+mx2﹣m=0,因為m>0,所以2lnx2+x2﹣1=0(*),
設函數h(x)=2lnx+x﹣1,因為當x>0時,h(x)是增函數,所以h(x)=0至多有一解.
因為h(1)=0,所以方程(*)的解為x2=1,即![]() =1,
=1,
解得m=![]() .
.


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:高中數學 來源: 題型:
| e | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2x |
| x+2 |
| 9 |
| 10 |
| 1 |
| e2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 5 | x+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 |
| 3 |
| 2 |
| x |
| 3 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com