
(本小題滿分14分)
已知函數(shù)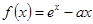 (
( 為常數(shù))的圖象與
為常數(shù))的圖象與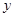 軸交于點
軸交于點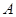 ,曲線
,曲線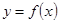 在點
在點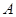 處
處
的切線斜率為-1.
(I)求 的值及函數(shù)
的值及函數(shù) 的極值;
的極值;
(II)證明:當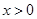 時,
時,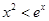 ;
;
(III)證明:對任意給定的正數(shù)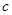 ,總存在
,總存在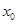 ,使得當
,使得當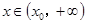 ,恒有
,恒有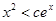 .
.
(I)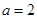 ,極值參考解析;(II)參考解析;(III)參考解析
,極值參考解析;(II)參考解析;(III)參考解析
解析試題分析:(I)由函數(shù)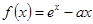 (
( 為常數(shù))的圖象與
為常數(shù))的圖象與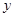 軸交于點
軸交于點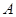 ,曲線
,曲線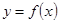 在點
在點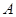 處
處
的切線斜率為-1.所以求函數(shù) 的導數(shù),即可求出
的導數(shù),即可求出 的值.再根據(jù)函數(shù)
的值.再根據(jù)函數(shù) 的導數(shù)地正負,即可得函數(shù)
的導數(shù)地正負,即可得函數(shù) 的極值.
的極值.
(II)當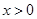 時,
時,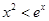 恒成立,等價轉換為函數(shù)的最值問題.令
恒成立,等價轉換為函數(shù)的最值問題.令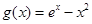 ,通過求函數(shù)
,通過求函數(shù)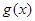 的導數(shù)求出最值即可得到結論.
的導數(shù)求出最值即可得到結論.
(III)對任意給定的正數(shù)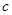 ,總存在
,總存在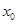 ,使得當
,使得當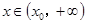 ,恒有
,恒有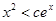 .由(II)得到函數(shù)的單調(diào)性當
.由(II)得到函數(shù)的單調(diào)性當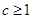 時,即可找到
時,即可找到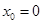 符合題意.當
符合題意.當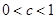 時.通過等價轉化,等價于不等式恒成立問題,再對通過估算得到
時.通過等價轉化,等價于不等式恒成立問題,再對通過估算得到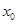 的值.即可得到結論.
的值.即可得到結論.
試題解析:(I)由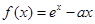 ,得
,得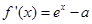 .又
.又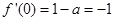 ,得
,得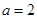 .所以
.所以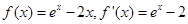 .令
.令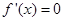 ,得
,得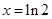 .當
.當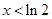 時,
時, 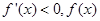 單調(diào)遞減;當
單調(diào)遞減;當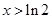 時,
時, 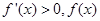 單調(diào)遞增.所以當
單調(diào)遞增.所以當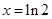 時,
時, 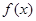 取得極小值,且極小值為
取得極小值,且極小值為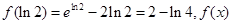 無極大值.
無極大值.
(II)令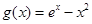 ,則
,則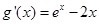 .由(I)得
.由(I)得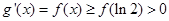 ,故
,故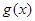 在R上單調(diào)遞增,又
在R上單調(diào)遞增,又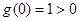 ,因此,當
,因此,當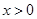 時,
時, 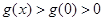 ,即
,即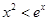 .
.
(III)①若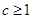 ,則
,則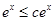 .又由(II)知,當
.又由(II)知,當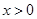 時,
時, 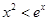 .所以當
.所以當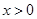 時,
時, 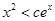 .取
.取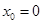 ,當
,當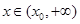 時,恒有
時,恒有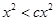 .
.
②若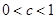 ,令
,令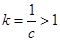 ,要使不等式
,要使不等式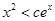 成立,只要
成立,只要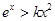 成立.而要使
成立.而要使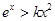 成立,則只要
成立,則只要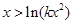 ,只要
,只要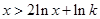 成立.令
成立.令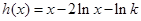 ,則
,則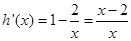 .所以當
.所以當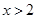 時,
時, 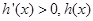 在
在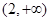 內(nèi)單調(diào)遞增.取
內(nèi)單調(diào)遞增.取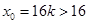 ,所以
,所以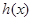 在
在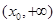 內(nèi)單調(diào)遞增.又
內(nèi)單調(diào)遞增.又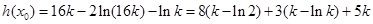 .易知
.易知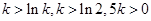 .所以
.所以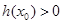 .即存在
.即存在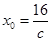 ,當
,當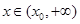 時,恒有
時,恒有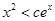 .
.
綜上,對任意給定的正數(shù)c,總存在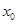 ,當
,當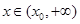 時,恒有
時,恒有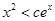 .
.
考點:1.函數(shù)的極值.2.構建新函數(shù)證


科目:高中數(shù)學 來源: 題型:解答題
(本小題滿分14分)
已知函數(shù)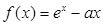 (
(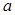 為常數(shù))的圖像與
為常數(shù))的圖像與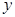 軸交于點
軸交于點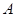 ,曲線
,曲線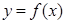 在點
在點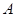 處的切線斜率為
處的切線斜率為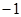 .
.
(1)求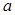 的值及函數(shù)
的值及函數(shù) 的極值;
的極值;
(2)證明:當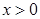 時,
時,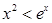
(3)證明:對任意給定的正數(shù)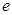 ,總存在
,總存在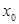 ,使得當
,使得當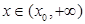 時,恒有
時,恒有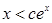
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
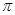 為圓周率,
為圓周率,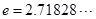 為自然對數(shù)的底數(shù).
為自然對數(shù)的底數(shù).
(1)求函數(shù)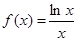 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)求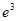 ,
,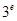 ,
,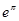 ,
,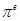 ,
, ,
,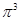 這6個數(shù)中的最大數(shù)與最小數(shù);
這6個數(shù)中的最大數(shù)與最小數(shù);
(3)將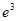 ,
,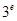 ,
,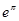 ,
,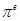 ,
, ,
,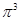 這6個數(shù)按從小到大的順序排列,并證明你的結論.
這6個數(shù)按從小到大的順序排列,并證明你的結論.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)f(x)=ax2+bln x在x=1處有極值 .
.
(1)求a,b的值;
(2)判斷函數(shù)y=f(x)的單調(diào)性并求出單調(diào)區(qū)間.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
用總長為14.8米的鋼條制成一個長方體容器的框架,如果所制的容器的底面的長比寬多0.5米,那么高為多少時容器的容器最大?并求出它的最大容積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù) .
.
(1)求 在區(qū)間
在區(qū)間 上的最大值;
上的最大值;
(2)若過點 存在3條直線與曲線
存在3條直線與曲線 相切,求t的取值范圍;
相切,求t的取值范圍;
(3)問過點 分別存在幾條直線與曲線
分別存在幾條直線與曲線 相切?(只需寫出結論)
相切?(只需寫出結論)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com