
設a=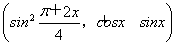 ,b=(4sinx,cosx-sinx),f(x)=a·b.
,b=(4sinx,cosx-sinx),f(x)=a·b.
(1)求函數f(x)的解析式;
(2)已知常數ω>0,若y=f(ωx)在區間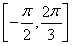 上是增函數,求ω的取值范圍;
上是增函數,求ω的取值范圍;
(3)設集合A=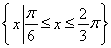 ,B={x||f(x)-m|<2},若A
,B={x||f(x)-m|<2},若A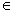 B,求實數m的取值范圍.
B,求實數m的取值范圍.
(1)f(x)=2sinx+1(2)ω∈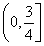 (3)m∈(1,4)
(3)m∈(1,4)
【解析】(1)f(x)=sin2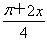 ·4sinx+(cosx+sinx)·(cosx-sinx)=4sinx·
·4sinx+(cosx+sinx)·(cosx-sinx)=4sinx· +cos2x
+cos2x
=2sinx(1+sinx)+1-2sin2x=2sinx+1,所以所求解析式為f(x)=2sinx+1.
(2)∵f(ωx)=2sinωx+1,ω>0,由2kπ-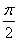 ≤ωx≤2kπ+
≤ωx≤2kπ+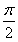 ,
,
得f(ωx)的增區間是 ,k∈Z.
,k∈Z.
∵f(ωx)在 上是增函數,∴
上是增函數,∴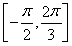
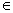
 .
.
∴-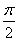 ≥-
≥-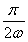 且
且 ≤
≤ ,∴ω∈
,∴ω∈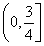 .
.
(3)由|f(x)-m|<2,得-2<f(x)-m<2,即f(x)-2<m<f(x)+2.
∵A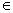 B,∴當
B,∴當 ≤x≤
≤x≤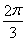 時,
時,
不等式f(x)-2<m<f(x)+2恒成立.∴f(x)max-2<m<f(x)min+2,
∵f(x)max=f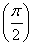 =3,f(x)min=f
=3,f(x)min=f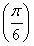 =2,∴m∈(1,4).
=2,∴m∈(1,4).


科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第三章第7課時練習卷(解析版) 題型:解答題
在△ABC中,a、b、c分別表示三個內角∠A、∠B、∠C的對邊,如果(a2+b2)sin(A-B)=(a2-b2)sin(A+B),判斷三角形的形狀.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第三章第5課時練習卷(解析版) 題型:解答題
已知α∈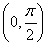 ,tanα=
,tanα=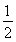 ,求:
,求:
(1)tan2α的值;
(2)sin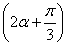 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第三章第4課時練習卷(解析版) 題型:解答題
已知α、β均為銳角,且sinα=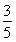 ,tan(α-β)=-
,tan(α-β)=-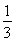 .
.
(1) 求sin(α-β)的值;
(2) 求cosβ的值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第三章第3課時練習卷(解析版) 題型:填空題
已知ω>0,函數f(x)=sin 在
在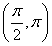 上單調遞減,則ω的取值范圍是________.
上單調遞減,則ω的取值范圍是________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第三章第3課時練習卷(解析版) 題型:解答題
已知函數f(x)=2 ·sin
·sin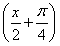 cos
cos -sin(x+π).
-sin(x+π).
(1)求f(x)的最小正周期;
(2)若將f(x)的圖象向右平移 個單位,得到函數g(x)的圖象,求函數g(x)在區間[0,π]上的最大值和最小值.
個單位,得到函數g(x)的圖象,求函數g(x)在區間[0,π]上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第三章第2課時練習卷(解析版) 題型:解答題
已知cos(π+α)=-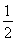 ,且角α在第四象限,計算:
,且角α在第四象限,計算:
(1)sin(2π-α);
(2)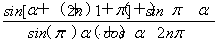 (n∈Z).
(n∈Z).
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第七章第3課時練習卷(解析版) 題型:填空題
設f(n)=1+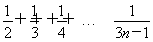 (n∈N*),則f(k+1)-f(k)=________.
(n∈N*),則f(k+1)-f(k)=________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com