
已知函數(shù)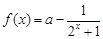 .
.
(1)確定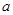 的值,使
的值,使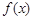 為奇函數(shù);
為奇函數(shù);
(2)當(dāng)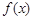 為奇函數(shù)時(shí),求
為奇函數(shù)時(shí),求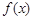 的值域。
的值域。
(1)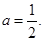 (2)
(2)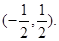
【解析】
試題分析:(1)  為奇函數(shù),
為奇函數(shù), 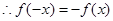 ,即
,即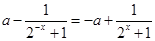 ,
,
解得: 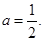
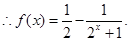 6
6
(2)由(1)知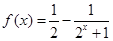 ,
, 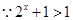 ,
,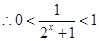 ,
,
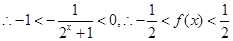
所以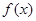 的值域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013100201044629746701/SYS201310020105492924485517_DA.files/image002.png">
12
的值域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013100201044629746701/SYS201310020105492924485517_DA.files/image002.png">
12
考點(diǎn):函數(shù)奇偶性和函數(shù)值域
點(diǎn)評:主要是考查了函數(shù)的奇函數(shù)定義的運(yùn)用,以及結(jié)合指數(shù)函數(shù)來得到值域,屬于中檔題。



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
| 1 |
| 2 |
| 1 |
| 4 |
| 1-m•2x |
| 1+m•2x |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| x2+2x+1 |
| x2+1 |
| A、2 | ||
B、
| ||
| C、1 | ||
D、
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
對于函數(shù)f(x),在使f(x)≤![]() M恒成立的所有常數(shù)M中,我們把M中的最小值稱為函數(shù)f(x)的“上確界”.已知函數(shù)f(x)=
M恒成立的所有常數(shù)M中,我們把M中的最小值稱為函數(shù)f(x)的“上確界”.已知函數(shù)f(x)=![]() +a(x∈[-2,2])是奇函數(shù),則f(x)的上確界為( )
+a(x∈[-2,2])是奇函數(shù),則f(x)的上確界為( )
A.2 B.![]()
C.1 D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013屆浙江寧波四校高二下學(xué)期期中聯(lián)考理科數(shù)學(xué)試卷(解析版) 題型:解答題
已知函數(shù) , 其中
, 其中 .
.
(1)當(dāng) 時(shí),求曲線
時(shí),求曲線 在點(diǎn)
在點(diǎn) 處的切線方程;
處的切線方程;
(2)當(dāng) 時(shí),求曲線
時(shí),求曲線 的單調(diào)區(qū)間與極值.
的單調(diào)區(qū)間與極值.
【解析】第一問中利用當(dāng) 時(shí),
時(shí), ,
,
 ,得到切線方程
,得到切線方程
第二問中,

對a分情況討論,確定單調(diào)性和極值問題。
解: (1) 當(dāng) 時(shí),
時(shí), ,
,
 ………………………….2分
………………………….2分

 切線方程為:
切線方程為:  …………………………..5分
…………………………..5分
(2) 
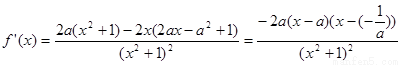 …….7
…….7 分
分
分類: 當(dāng) 時(shí), 很顯然
時(shí), 很顯然
 的單調(diào)增區(qū)間為:
的單調(diào)增區(qū)間為:  單調(diào)減區(qū)間:
單調(diào)減區(qū)間:  ,
,
 ,
,  ………… 11分
………… 11分
當(dāng)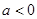 時(shí)
時(shí) 的單調(diào)減區(qū)間:
的單調(diào)減區(qū)間:  單調(diào)增區(qū)間:
單調(diào)增區(qū)間: 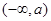 ,
,

 ,
, 
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:臺州一模 題型:單選題
| x2+2x+1 |
| x2+1 |
| A.2 | B.
| C.1 | D.
|
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com