
機床廠今年年初用98萬元購進一臺數控機床,并立即投入生產使用,計劃第一年維修、保養費用12萬元,從第二年開始,每年所需維修、保養費用比上一年增加4萬元,該機床使用后,每年的總收入為50萬元,設使用x年后數控機床的盈利額為y萬元.
(Ⅰ)寫出y與x之間的函數關系式;
(Ⅱ)從第幾年開始,該機床開始盈利(盈利額為正值);
(Ⅲ)使用若干年后,對機床的處理方案有兩種:
(1)當年平均盈利額達到最大值時,以30萬元價格處理該機床;
(2)當盈利額達到最大值時,以12萬元價格處理該機床.
請你研究一下哪種方案處理較為合理?請說明理由.
(Ⅰ) 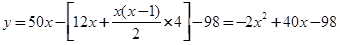 ;(Ⅱ)從第3年開始盈利;(Ⅲ)方案Ⅰ比較合理.
;(Ⅱ)從第3年開始盈利;(Ⅲ)方案Ⅰ比較合理.
解析試題分析:(Ⅰ)使用x年的總收入為 ,每年支付的維修保養費用構成一等差數列,由等差數列求和公式可得使用x年的總支出,總收入減去總支出便可得使用x年后數控機床的盈利額,從而得y與x之間的函數關系式.
,每年支付的維修保養費用構成一等差數列,由等差數列求和公式可得使用x年的總支出,總收入減去總支出便可得使用x年后數控機床的盈利額,從而得y與x之間的函數關系式.
(Ⅱ)解不等式 便可得
便可得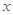 的范圍,從而知道從從第幾年開始盈利.
的范圍,從而知道從從第幾年開始盈利.
(Ⅲ))(1)年平均盈利額為: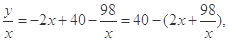
對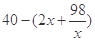 可用重要不等式求出其最大值,從而可確定什么時候年平均盈利額達到最大值,可求出工廠獲得的總利潤.
可用重要不等式求出其最大值,從而可確定什么時候年平均盈利額達到最大值,可求出工廠獲得的總利潤.
(2)盈利額y=-2x2+40x-98是一個二次函數,可通過配方求出其最大值,從而可確定什么時候盈利額達到最大值,可求出工廠獲得的總利潤.
將二者進行比較,便知哪個方案更合理.
試題解析:(Ⅰ)依題得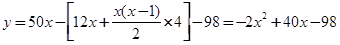 (x
(x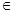 N*). 3分
N*). 3分
(Ⅱ)解不等式 得
得 .
.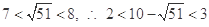 .又∵x
.又∵x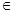 N*,∴3≤x≤17,故從第3年開始盈利. 7分
N*,∴3≤x≤17,故從第3年開始盈利. 7分
(Ⅲ)(1)年平均盈利額為: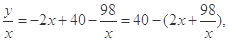
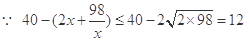 ,當且僅當
,當且僅當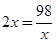 時,即x=7時等號成立.
時,即x=7時等號成立.
所以到2008年,年平均盈利額達到最大值,工廠共獲利12×7+30=114萬元.
(2)盈利額y=-2x2+40x-98=-(x-10)2+102,當x=10時,ymax=102.
故到2011年,盈利額達到最大值,工廠獲利102+12=114萬元 .
盈利額達到的最大值相同,而方案Ⅰ所用的時間較短,故方案Ⅰ比較合理. 12分
考點:1、函數的應用;2、函數的最值;3、重要不等式.


科目:高中數學 來源: 題型:解答題
如圖,某生態園欲把一塊四邊形地 辟為水果園,其中
辟為水果園,其中 ,
, 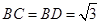 ,
, .若經過
.若經過 上一點
上一點 和
和 上一點
上一點 鋪設一條道路
鋪設一條道路 ,且
,且 將四邊形
將四邊形 分成面積相等的兩部分,設
分成面積相等的兩部分,設 .
.
(1)求 的關系式;
的關系式;
(2)如果 是灌溉水管的位置,為了省錢,希望它最短,求
是灌溉水管的位置,為了省錢,希望它最短,求 的長的最小值;
的長的最小值;
(3)如果 是參觀路線,希望它最長,那么
是參觀路線,希望它最長,那么 的位置在哪里?
的位置在哪里?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com