
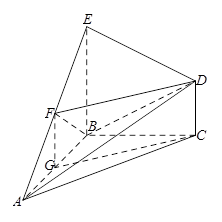
如圖,在幾何體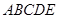 中,
中, 平面
平面 ,
,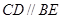 ,
,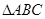 是等腰直角三角形,
是等腰直角三角形,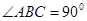 ,且
,且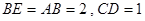 ,點
,點 是
是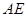 的中點.
的中點.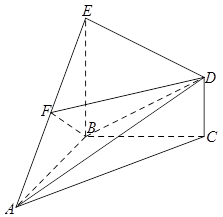
(Ⅰ)求證: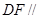 平面
平面 ;
;
(Ⅱ)求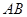 與平面
與平面 所成角的正弦值.
所成角的正弦值.
(Ⅰ)詳見解析;(Ⅱ)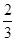 .
.
解析試題分析:(Ⅰ)證法一是取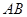 的中點
的中點 ,構造四邊形
,構造四邊形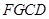 ,并證明四邊形
,并證明四邊形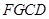 為平行四邊形,得到
為平行四邊形,得到 ,從而證明
,從而證明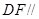 平面
平面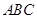 ;證法二是取
;證法二是取 的中點
的中點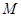 ,構造平面
,構造平面 ,通過證明平面
,通過證明平面 平面
平面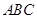 ,并利用平面與平面平行的性質來證明
,并利用平面與平面平行的性質來證明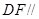 平面
平面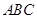 ;(Ⅱ)直接利用空間向量法求直線
;(Ⅱ)直接利用空間向量法求直線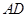 與平面
與平面 所成角的正弦值.
所成角的正弦值.
試題解析:解法一:(Ⅰ)取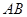 的中點
的中點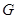 ,連結
,連結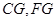 ,
,
則 ,且
,且 , 2分
, 2分
又 ,∴
,∴ 且
且 ,所以四邊形
,所以四邊形 是平行四邊形,
是平行四邊形,
則 , 5分
, 5分
又因為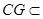 平面
平面 ,
, 平面
平面 ,所以
,所以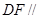 平面
平面 . 6分
. 6分
(Ⅱ)依題得,以點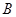 為原點,
為原點, 所在的直線分別為
所在的直線分別為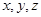 軸,建立如圖的空間直角坐標系,
軸,建立如圖的空間直角坐標系,
則 ,
, ,
,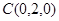 ,
, ,
,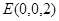 ,
,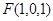 ,
,
所以 ,
,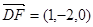 .
.
設平面 的一個法向量為
的一個法向量為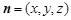 ,則
,則 即
即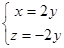 ,
,
取 ,得,
,得, . 10分
. 10分
又設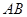 與平面
與平面 所成的角為
所成的角為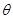 ,
, ,
,
則 ,
,
故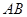 與平面
與平面 所成角的正弦值為
所成角的正弦值為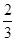 . 13分
. 13分
解法二:(Ⅰ)取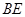 的中點
的中點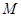 ,連結
,連結 ,
,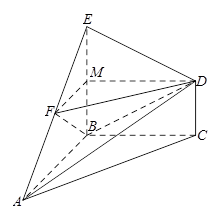
則 ,
,
又因為 平面
平面 ,
,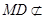 平面
平面 ,
, 平面
平面


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
如圖已知:菱形 所在平面與直角梯形
所在平面與直角梯形 所在平面互相垂直,
所在平面互相垂直, ,
, 點
點 分別是線段
分別是線段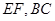 的中點.
的中點. 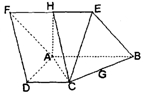
(1)求證:平面
 平面
平面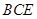 ;
;
(2)點 在直線
在直線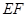 上,且
上,且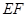 //平面
//平面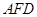 ,求平面
,求平面 與平面
與平面 所成角的余弦值。
所成角的余弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知直角梯形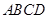 中,
中,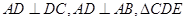 是邊長為2的等邊三角形,
是邊長為2的等邊三角形,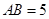 .沿
.沿 將
將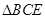 折起,使
折起,使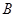 至
至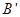 處,且
處,且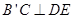 ;然后再將
;然后再將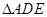 沿
沿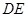 折起,使
折起,使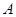 至
至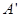 處,且面
處,且面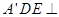 面
面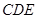 ,
,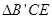 和
和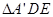 在面
在面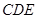 的同側.
的同側.

(Ⅰ) 求證: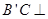 平面
平面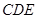 ;
;
(Ⅱ) 求平面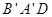 與平面
與平面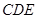 所構成的銳二面角的余弦值.
所構成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,平面四邊形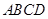 的4個頂點都在球
的4個頂點都在球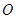 的表面上,
的表面上,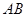 為球
為球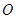 的直徑,
的直徑, 為球面上一點,且
為球面上一點,且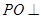 平面
平面 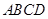 ,
,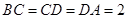 ,點
,點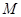 為
為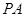 的中點.
的中點.
(1) 證明:平面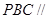 平面
平面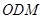 ;
;
(2) 求平面 與平面
與平面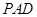 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2。將△ABD沿邊AB折起, 使得△ABD與△ABC成30o的二面角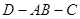 ,如圖二,在二面角
,如圖二,在二面角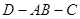 中.
中.
(1) 求CD與面ABC所成的角正弦值的大小;
(2) 對于AD上任意點H,CH是否與面ABD垂直。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com