
如圖所示,已知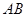 為圓
為圓 的直徑,點
的直徑,點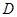 為線段
為線段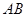 上一點,且
上一點,且 ,點
,點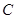 為圓
為圓 上一點,且
上一點,且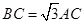 .點
.點 在圓
在圓 所在平面上的正投影為點
所在平面上的正投影為點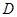 ,
, .
.
(1)求證: ;
;
(2)求二面角 的余弦值.
的余弦值.
(1)詳見解析;(2)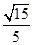
解析試題分析:(1)要證 ,需先證
,需先證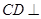 平面
平面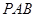 ,由于
,由于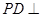 平面
平面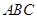 易證,故有
易證,故有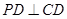 ,又因為
,又因為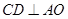 ,則證得
,則證得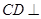 平面
平面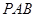 ;(2)綜合法是先找到二面角的一個平面角
;(2)綜合法是先找到二面角的一個平面角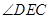 ,不過必須根據(jù)平面角的定義證明,然后在
,不過必須根據(jù)平面角的定義證明,然后在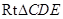 中解出
中解出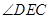 的三角函數(shù)值.
的三角函數(shù)值.
試題解析:(1)連接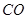 ,由
,由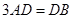 知,點
知,點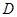 為
為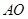 的中點,
的中點,
又∵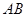 為圓
為圓 的直徑,∴
的直徑,∴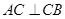 ,
,
由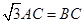 知,
知, ,
,
∴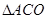 為等邊三角形,從而
為等邊三角形,從而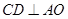 . 3分
. 3分
∵點 在圓
在圓 所在平面上的正投影為點
所在平面上的正投影為點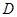 ,
,
∴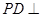 平面
平面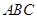 ,又
,又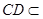 平面
平面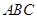 ,
,
∴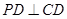 , 5分
, 5分
由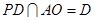 得,
得,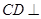 平面
平面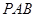 ,
,
又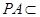 平面
平面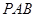 ,
,
∴ . 6分
. 6分
(2)(綜合法)過點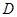 作
作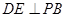 ,垂足為
,垂足為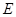 ,連接
,連接 . 7分
. 7分
由(1)知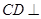 平面
平面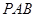 ,又
,又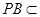 平面
平面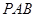 ,
,
∴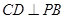 ,又
,又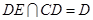 ,
,
∴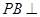 平面
平面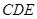 ,又
,又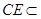 平面
平面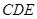 ,∴
,∴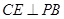 , 9分
, 9分
∴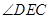 為二面角
為二面角 的平面角. 10分
的平面角. 10分
由(Ⅰ)可知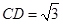 ,
, ,
,
∴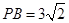 ,則
,則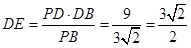 ,
,
∴在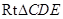 中,
中,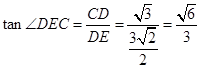 ,
,
∴ ,即二面角
,即二面角 的余弦值為
的余弦值為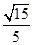 . 14分
. 14分
考點:1、線線垂直和線面垂直的證明,2、二面角的計算.


 狀元坊全程突破導(dǎo)練測系列答案
狀元坊全程突破導(dǎo)練測系列答案 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,AB為圓O的直徑,點E、F在圓O上,且AB∥EF,矩形ABCD所在的平面與圓O所在的平面互相垂直,已知AB=2,AD=EF=1.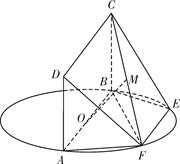
(Ⅰ)設(shè)FC的中點為M,求證:OM∥平面DAF;
(Ⅱ)設(shè)平面CBF將幾何體EF-ABCD分割成的兩個錐體的體積分別為VF-ABCD、VF-CBE,求VF-ABCD:VF-CBE的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖所示的幾何體ABCDFE中,△ABC,△DFE都是等邊三角形,且所在平面平行,四邊形BCED是邊長為2的正方形,且所在平面垂直于平面ABC.
(Ⅰ)求幾何體ABCDFE的體積;
(Ⅱ)證明:平面ADE∥平面BCF;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,四棱錐F-ABCD的底面ABCD是菱形,其對角線AC=2,BD= ,AE、CF都與平面ABCD垂直,AE=1,CF=2.
,AE、CF都與平面ABCD垂直,AE=1,CF=2.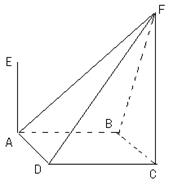
(I)求二面角B-AF-D的大小;
(II)求四棱錐E-ABCD與四棱錐F-ABCD公共部分的體積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com