
(08年福建卷文)(本小題滿分14分)
如圖,橢圓![]() 的一個(gè)焦點(diǎn)是
的一個(gè)焦點(diǎn)是![]() ,且過點(diǎn)
,且過點(diǎn)![]() 。
。
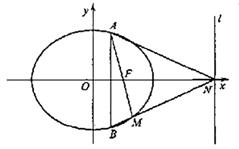
(Ⅰ)求橢圓C的方程;
(Ⅱ)若AB為垂直于x軸的動弦,直線![]() 與x軸交于點(diǎn)N,直線AF與BN交于點(diǎn)M。
與x軸交于點(diǎn)N,直線AF與BN交于點(diǎn)M。
()求證:點(diǎn)M恒在橢圓C上;
()求![]() 面積的最大值。
面積的最大值。
解析:本小題主要考查直線與橢圓的位置關(guān)系、軌跡方程、不等式等基本知識,考查運(yùn)算能力和綜合解題能力。
解法一:
(Ⅰ)由題設(shè)![]() ,從而
,從而![]() ,
,
所以橢圓C的方程為![]() 。
。
(Ⅱ)()由題意得![]() 。
。
設(shè)![]() 則
則![]() ,
,![]() 。 ……………………………… ①
。 ……………………………… ①
![]() 與
與![]() 的方程分別為:
的方程分別為:![]()
![]() 。
。
設(shè)![]() ,則有
,則有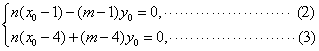
由②,③得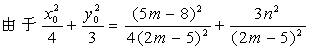
![]() 。
。
![]()
![]()
![]() 。
。
所以點(diǎn)M恒在橢圓C上。
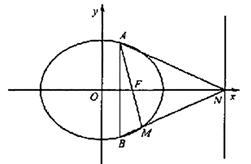
()設(shè)AM的方程為![]() ,代入
,代入![]() 得
得![]() 。
。
設(shè)![]() ,則有:
,則有:![]() 。
。
![]() 。
。
令![]() ,則
,則
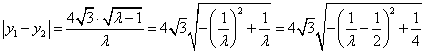 ,
,
因?yàn)?IMG height=19 src='http://thumb.zyjl.cn/pic1/img/20090323/20090323113702028.gif' width=39>,![]()
![]() 有最大值3,此時(shí)AM過點(diǎn)F。
有最大值3,此時(shí)AM過點(diǎn)F。
△AMN的面積![]() 有最大值
有最大值![]() 。
。
解法二:
(Ⅰ)同解法一:
(Ⅱ)()由題意得![]() 。
。
設(shè)![]() 則
則![]() ,
,![]() 。 ……………………………… ①
。 ……………………………… ①
![]() 與
與![]() 的方程分別為:
的方程分別為:![]() …………………………… ②
…………………………… ②
![]() …………………………… ③
…………………………… ③
由②,③得:當(dāng)![]() 時(shí),
時(shí),![]() 。………………………… ④
。………………………… ④
由④代入①,得![]() 。
。
當(dāng)![]() 時(shí),由②,③得:
時(shí),由②,③得: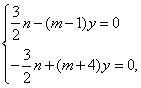
解得![]() 與
與![]() 矛盾。
矛盾。
所以點(diǎn)M的軌跡方程為![]() 即點(diǎn)M恒在橢圓C上。
即點(diǎn)M恒在橢圓C上。
(Ⅱ)同解法一。



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
(08年福建卷文)(本小題滿分12分)
已知函數(shù)![]() 的圖象過點(diǎn)
的圖象過點(diǎn)![]() ,且函數(shù)
,且函數(shù)![]() 的圖象關(guān)于y軸對稱。
的圖象關(guān)于y軸對稱。
(Ⅰ)求![]() 的值及函數(shù)
的值及函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若![]() ,求函數(shù)
,求函數(shù)![]() 在區(qū)間
在區(qū)間![]() 內(nèi)的極值。
內(nèi)的極值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(08年福建卷文)(本小題滿分12分)
已知{an}是正數(shù)組成的數(shù)列,a1=1,且點(diǎn)(![]() )(n
)(n![]() N*)在函數(shù)y=x2+1的圖象上.
N*)在函數(shù)y=x2+1的圖象上.
(Ⅰ)求數(shù)列{an}的通項(xiàng)公式;
(Ⅱ)若列數(shù){bn}滿足b1=1,bn+1=bn+![]() ,求證:
,求證:![]() 。
。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(08年福建卷文)(本小題滿分12分)
已知{an}是正數(shù)組成的數(shù)列,a1=1,且點(diǎn)(![]() )(n
)(n![]() N*)在函數(shù)y=x2+1的圖象上.
N*)在函數(shù)y=x2+1的圖象上.
(Ⅰ)求數(shù)列{an}的通項(xiàng)公式;
(Ⅱ)若列數(shù){bn}滿足b1=1,bn+1=bn+![]() ,求證:
,求證:![]() 。
。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(08年福建卷文)(本小題滿分12分)
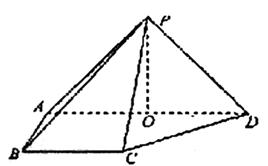
如圖,在四棱錐P―ABCD中,側(cè)面PAD⊥底面ABCD,側(cè)棱PA=PD=![]() ,底面ABCD為直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O為AD中點(diǎn).
,底面ABCD為直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O為AD中點(diǎn).
(Ⅰ)求證:PO⊥平面ABCD;
(Ⅱ)求異面直線PB與CD所成角的余弦值;
(Ⅲ)求點(diǎn)A到平面PCD的距離。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(08年福建卷文)(本小題滿分12分)
如圖,在四棱錐P―ABCD中,側(cè)面PAD⊥底面ABCD,側(cè)棱PA=PD=![]() ,底面ABCD為直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O為AD中點(diǎn).
,底面ABCD為直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O為AD中點(diǎn).
(Ⅰ)求證:PO⊥平面ABCD;
(Ⅱ)求異面直線PB與CD所成角的余弦值;
(Ⅲ)求點(diǎn)A到平面PCD的距離。

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com