
設(shè)橢圓的方程為![]() =1(m,n>0),過(guò)原點(diǎn)且傾角為θ和π-θ(0<θ<
=1(m,n>0),過(guò)原點(diǎn)且傾角為θ和π-θ(0<θ<![]() =的兩條直線分別交橢圓于A、C和B、D兩點(diǎn),
=的兩條直線分別交橢圓于A、C和B、D兩點(diǎn),
(Ⅰ)用θ、m、n表示四邊形ABCD的面積S;
(Ⅱ)若m、n為定值,當(dāng)θ在(0,![]() ]上變化時(shí),求S的最小值u;
]上變化時(shí),求S的最小值u;
(Ⅲ)如果μ>mn,求![]() 的取值范圍.
的取值范圍.
解:(Ⅰ)設(shè)經(jīng)過(guò)原點(diǎn)且傾角為θ的直線方程為y=xtanθ,可得方程組 (Ⅱ)S= (1)當(dāng)m>n,即 由于0<θ≤ 故tanθ= (2)當(dāng)m<n,即 由于
因?yàn)?<tanθ1<tanθ2≤1,m2tanθ1tanθ2-n2<m2-n2<0,所以(m2tanθ2+ 所以u= (Ⅲ)(1)當(dāng) (2)當(dāng) 所以 得 綜上,當(dāng)u>mn時(shí), |



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源:數(shù)學(xué)教研室 題型:044
(Ⅰ)用θ、m、n表示四邊形ABCD的面積S;
(Ⅱ)若m、n為定值,當(dāng)θ在(0,![]() ]上變化時(shí),求S的最小值u;
]上變化時(shí),求S的最小值u;
(Ⅲ)如果μ>mn,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2007年綜合模擬數(shù)學(xué)卷三 題型:044
設(shè)橢圓C1的方程為![]() =1,(a>b>0).曲線C2的方程為y=
=1,(a>b>0).曲線C2的方程為y=![]() .且C1與C2在第一象限內(nèi)只有一個(gè)公共點(diǎn)P.
.且C1與C2在第一象限內(nèi)只有一個(gè)公共點(diǎn)P.
(1)試用a表示點(diǎn)P的坐標(biāo);
(2)設(shè)A,B是橢圓C1的兩個(gè)焦點(diǎn),當(dāng)a變化時(shí),求△ABP的面積函數(shù)S(a)的值域;
(3)記min{y1,y2…yn}為y1,y2…yn中最小的一個(gè),設(shè)g(a)是以橢圓C1的半焦距為邊長(zhǎng)的正方形的面積,試求函數(shù)f(a)=min{g(a),S(a)}的表達(dá)式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:高考零距離 二輪沖刺優(yōu)化講練 數(shù)學(xué) 題型:044
| |||||||||||||||
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2010年全國(guó)普通高等學(xué)校招生統(tǒng)一考試、文科數(shù)學(xué)(上海卷) 題型:044
已知橢圓 的方程為
的方程為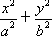 =1(a>b>0),A(0,b)、B(0,-b)和Q(a,0)為
=1(a>b>0),A(0,b)、B(0,-b)和Q(a,0)為 的三個(gè)頂點(diǎn).
的三個(gè)頂點(diǎn).
(1)若點(diǎn)M滿足![]() ,求點(diǎn)M的坐標(biāo);
,求點(diǎn)M的坐標(biāo);
(2)設(shè)直線l1∶y=k1x+p交橢圓 于C、D兩點(diǎn),交直線l2∶y=k2x于點(diǎn)E.若k1·k2=
于C、D兩點(diǎn),交直線l2∶y=k2x于點(diǎn)E.若k1·k2= ,證明:E為CD的中點(diǎn);
,證明:E為CD的中點(diǎn);
(3)設(shè)點(diǎn)P在橢圓 內(nèi)且不在x軸上,如何構(gòu)作過(guò)PQ中點(diǎn)F的直線l,使得l與橢圓
內(nèi)且不在x軸上,如何構(gòu)作過(guò)PQ中點(diǎn)F的直線l,使得l與橢圓 的兩個(gè)交點(diǎn)P1,P2滿足
的兩個(gè)交點(diǎn)P1,P2滿足![]() ?令a=10,b=5,點(diǎn)P的坐標(biāo)是(-8,-1).若橢圓
?令a=10,b=5,點(diǎn)P的坐標(biāo)是(-8,-1).若橢圓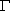 上的點(diǎn)P1,P2滿足
上的點(diǎn)P1,P2滿足![]() ,求點(diǎn)P1,P2的坐標(biāo).
,求點(diǎn)P1,P2的坐標(biāo).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com