
已知定義在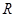 的函數(shù)
的函數(shù)
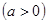 在區(qū)間
在區(qū)間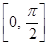 上的值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/85/7/4xxhi.png" style="vertical-align:middle;" />,
上的值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/85/7/4xxhi.png" style="vertical-align:middle;" />,
(Ⅰ)求 、
、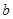 的值;
的值;
(Ⅱ)求函數(shù)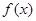 的最小正周期;
的最小正周期;
(Ⅲ)求函數(shù)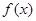 的單調(diào)減區(qū)間.
的單調(diào)減區(qū)間.
(Ⅰ) 、
、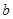 的值分別為3,
的值分別為3,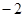 (Ⅱ)
(Ⅱ) (Ⅲ)
(Ⅲ)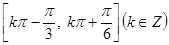
解析試題分析:(Ⅰ)
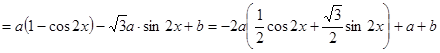
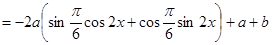
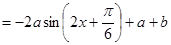
∵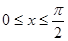 ,∴
,∴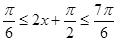 ,∴
,∴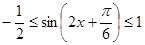 ,又
,又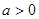
∴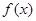 的值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/b4/6/1mzq83.png" style="vertical-align:middle;" />,根據(jù)題設(shè)條件
的值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/b4/6/1mzq83.png" style="vertical-align:middle;" />,根據(jù)題設(shè)條件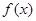 值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/85/7/4xxhi.png" style="vertical-align:middle;" />,
值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/85/7/4xxhi.png" style="vertical-align:middle;" />,
故有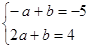 ,解得
,解得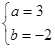 ,所以所求
,所以所求 、
、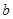 的值分別為3,
的值分別為3,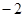 。
。
(Ⅱ)由(1)得 ,∴
,∴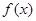 的最小正周期為
的最小正周期為 。
。
(Ⅲ)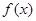 的單調(diào)減區(qū)間即為函數(shù)
的單調(diào)減區(qū)間即為函數(shù)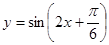 的單調(diào)增區(qū)間,
的單調(diào)增區(qū)間,
由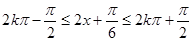 ,得
,得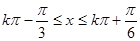
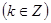 ,
,
故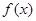 的單調(diào)減區(qū)間為
的單調(diào)減區(qū)間為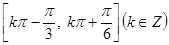 .
.
考點(diǎn):三角函數(shù)的最值三角函數(shù)的周期性及求法
點(diǎn)評:本題考查的知識點(diǎn)是三角函數(shù)的最值,三角函數(shù)的周期性及其求法,其中根據(jù)降冪公式(逆用二倍角公式)及輔助角公式,我將函數(shù)解析式化為正弦型函數(shù)的形式,是解答本題的關(guān)鍵.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
函數(shù) 的一段圖象如圖所示.
的一段圖象如圖所示.
(1)求函數(shù) 的解析式;
的解析式;
(2)將函數(shù) 的圖象向右平移
的圖象向右平移 個單位,得到
個單位,得到 的圖象,求直線
的圖象,求直線 與函數(shù)
與函數(shù) 的圖象在
的圖象在 內(nèi)所有交點(diǎn)的坐標(biāo).
內(nèi)所有交點(diǎn)的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,某機(jī)場建在一個海灣的半島上,飛機(jī)跑道AB的長為4.5km,且跑道所在直線與海岸線,的夾角為60°(海岸線看作直線),跑道上距離海岸線最近的點(diǎn)B到海岸線的距離BC=4 ,D為海岸線l上的一點(diǎn).設(shè)CD=xkm(x>
,D為海岸線l上的一點(diǎn).設(shè)CD=xkm(x> ),點(diǎn)D對跑道AB的視角為
),點(diǎn)D對跑道AB的視角為 .
.
(1)將tan 表示為x的函數(shù):
表示為x的函數(shù):
(2)求點(diǎn)D的位置,使得 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)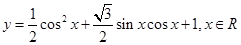
(1)當(dāng)函數(shù)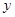 取得最大值時,求自變量
取得最大值時,求自變量 的取值集合;
的取值集合;
(2)求該函數(shù)的單調(diào)遞增區(qū)間。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
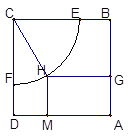
在申辦國家級示范性高中期間,某校擬用運(yùn)動場的邊角地建一個矩形的健身室. 如圖所示,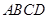 是一塊邊長為50m的正方形地皮,扇形
是一塊邊長為50m的正方形地皮,扇形 是運(yùn)動場的一部分,其半徑為40m,矩形
是運(yùn)動場的一部分,其半徑為40m,矩形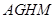 就是擬建的健身室,其中
就是擬建的健身室,其中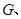
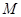 分別在
分別在 和
和 上,
上,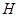 在弧
在弧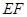 上,設(shè)矩形
上,設(shè)矩形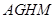 的面積為
的面積為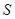 ,∠
,∠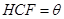 .
.
(1) 試將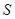 表示為
表示為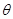 的函數(shù);
的函數(shù);
(2) 當(dāng)點(diǎn)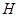 在弧
在弧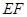 的何處時,該健身室的面積最大?最大面積為多少?
的何處時,該健身室的面積最大?最大面積為多少?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com