
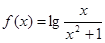 ,有下列結論:①函數
,有下列結論:①函數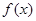 的定義域是(0,+∞);②函數
的定義域是(0,+∞);②函數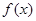 是奇函數;③函數
是奇函數;③函數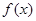 的最小值為-
的最小值為-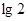 ;④當
;④當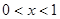 時,函數
時,函數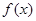 是增函數;當
是增函數;當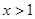 時,函數
時,函數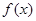 是減函數.
是減函數. 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:不詳 題型:解答題
 (單位:千克/年)是養殖密度
(單位:千克/年)是養殖密度 (單位:尾/立方米)的函數.當
(單位:尾/立方米)的函數.當 不超過4(尾/立方米)時,
不超過4(尾/立方米)時, 的值為
的值為 (千克/年);當
(千克/年);當 時,
時, 是
是 的一次函數;當
的一次函數;當 達到
達到 (尾/立方米)時,因缺氧等原因,
(尾/立方米)時,因缺氧等原因, 的值為
的值為 (千克/年).
(千克/年). 時,求函數
時,求函數 的表達式;
的表達式; 為多大時,魚的年生長量(單位:千克/立方米)
為多大時,魚的年生長量(單位:千克/立方米) 可以達到最大,并求出最大值.
可以達到最大,并求出最大值.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
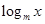 (m為常數0<m<1),且數列{f(
(m為常數0<m<1),且數列{f( )}是首項為2,公差為2的等差數列.
)}是首項為2,公差為2的等差數列.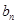 =
= f(
f( ),當m=
),當m=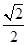 時,求數列{
時,求數列{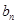 }的前n項和
}的前n項和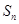 ;
; =
= ·
·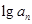 ,如果{
,如果{ }中的每一項恒小于它后面的項,求m的取值范圍.
}中的每一項恒小于它后面的項,求m的取值范圍.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題

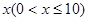 分鐘應付話費y元,寫出函數解析式并畫出函數圖象.
分鐘應付話費y元,寫出函數解析式并畫出函數圖象.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
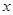 %,則銷售量將減少
%,則銷售量將減少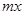 %,且該化工產品每噸的價格上漲幅度不超過
%,且該化工產品每噸的價格上漲幅度不超過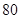 %,
%,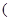 其中
其中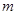 為正常數
為正常數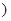

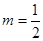 時,該產品每噸的價格上漲百分之幾,可使銷售的總金額最大?
時,該產品每噸的價格上漲百分之幾,可使銷售的總金額最大?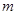 的取值范圍.
的取值范圍.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com