Question

（本題滿分12分）
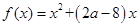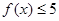已知函數，不等式的解集是．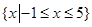
（1）求實數的值；
（2）對于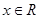恒成立，求實數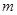的取值范圍．

Answer 1

（1）；
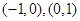（2）的單調遞增區間是，單調遞減區間是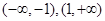．（12分）

解析試題分析：（1）根據二次函數的不等式的解集，結合韋達定理可知參數a,b的值，求解解析式。
（2）要使得不等式對于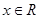恒成立，，只要求解函數f(x)的最小值即可。轉化與劃歸思想的運用。
解（1）設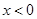，則，
所以（3分）
又是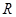上的奇函數，則，（4分）
所以，（6分）
（2）函數的圖像略
（畫圖像關鍵點必須畫準確，如頂點、端點、點的虛實，變化趨勢等9分）
根據函數的圖像可知，的單調遞增區間是，
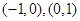單調遞減區間是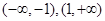．（12分）
考點：本題主要考查了一元二次不等式的應用，二次函數性質的運用。體現了分類討論的數學思想．
點評：解決該試題的關鍵是能結合不等式的解集得到參數的取值進而得到解析式，而對于恒成立的問題，通常轉化為最大值或者最小值問題來處理即可。