
(本題12分)已知曲線y=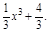
(1)求曲線在x=2處的切線方程;(2)求曲線過點(2,4)的切線方程.
(1)4x-y-4="0." (2)4x-y-4=0或x-y+2=0.
【解析】
試題分析:(1)∵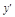 =x2,∴在點P(2,4)處的切線的斜率k=
=x2,∴在點P(2,4)處的切線的斜率k=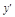 |x=2="4." ……………2分
|x=2="4." ……………2分
∴曲線在點P(2,4)處的切線方程為y-4=4(x-2),即4x-y-4="0." …………………… 4分
(2)設曲線y=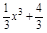 與過點P(2,4)的切線相切于點
與過點P(2,4)的切線相切于點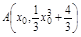 ,
,
則切線的斜率k=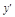 |
|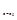 =
=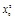 . ……………… 6分
. ……………… 6分
∴切線方程為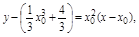 即
即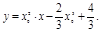 ……………………
8分
……………………
8分
∵點P(2,4)在切線上,∴4=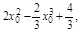
即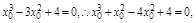 ∴
∴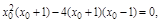
∴(x0+1)(x0-2)2=0,解得x0=-1或x0=2,
故所求的切線方程為4x-y-4=0或x-y+2=0. ……………………12分
考點:本題主要考查導數的幾何意義。
點評:易錯題,求曲線的切線問題,往往包括兩種類型,一是知切點,二是過曲線外的點,后者難度大些。


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源:2011年廣東省揭陽市第一中學高二上學期期末檢測數學理卷 題型:解答題
本題12分)已知 且
且 ,命題P:函數
,命題P:函數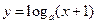 在區間
在區間 上為減函數;命題Q:曲線
上為減函數;命題Q:曲線 與
與 軸相交于不同的兩點.若“
軸相交于不同的兩點.若“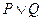 ”為真,“
”為真,“ ”為假,求實數
”為假,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2013屆云南省高二下學期期中文科數學試卷(解析版) 題型:解答題
(本題12分)已知函數 ,其中
,其中 .
.
(Ⅰ)若曲線 在點
在點 處的切線方程為
處的切線方程為 ,求函數
,求函數 的解析式;
的解析式;
(Ⅱ)討論函數 的單調性;
的單調性;
(Ⅲ)若對于任意的 ,不等式
,不等式 在
在 上恒成立,求
上恒成立,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2013屆河北省高二上學期四調理科數學 題型:解答題
(本題滿分12分)已知曲線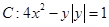
(I)若直線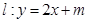 與曲線
與曲線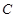 只有一個公共點,求實數
只有一個公共點,求實數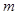 的取值范圍;
的取值范圍;
(II)若直線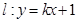 與曲線
與曲線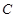 恒有兩個不同的交點
恒有兩個不同的交點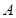 和
和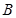 ,且
,且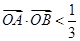 (其中
(其中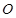 為坐標原點),求實數
為坐標原點),求實數 的取值范圍。
的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com