
設函數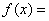
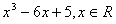 .
.
(1)求函數 的單調區間和極值。
的單調區間和極值。
(2)若關于 的方程
的方程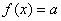 有三個不同實根,求實數
有三個不同實根,求實數 的取值范圍;
的取值范圍;
(3)已知當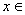 (1,+∞)時,
(1,+∞)時,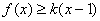 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.
(1)f(x)的單調遞增區間為(-∞,- )和(
)和( ,+∞);單調減區間為(-
,+∞);單調減區間為(- ,
, ).當x=-
).當x=- 時,f(x)有極大值5+4
時,f(x)有極大值5+4 ;當x=
;當x= 時,f(x)有極小值5-4
時,f(x)有極小值5-4 .
.
(2)-4 <a<5+4
<a<5+4
(3)k≤-3
解析試題分析:(1) 解:f′(x)=3x2-6,令f′(x)=0,解得x1=- ,x2=
,x2= .
.
因為當x> 或x<-
或x<- 時,f′(x)>0;當-
時,f′(x)>0;當- <x<
<x< 時,f′(x)<0.
時,f′(x)<0.
所以f(x)的單調遞增區間為(-∞,- )和(
)和( ,+∞);單調減區間為(-
,+∞);單調減區間為(- ,
, ).
).
當x=- 時,f(x)有極大值5+4
時,f(x)有極大值5+4 ;
;
當x= 時,f(x)有極小值5-4
時,f(x)有極小值5-4 . ---————-3分
. ---————-3分
(2)由(1)的分析知 y=f(x)的圖象的大致形狀及走向如圖所示,當5-4 <a<5+4
<a<5+4 時,直線y=a與y=f(x)的圖象有三個不同交點,即方程f(x)=a有三個不同的
時,直線y=a與y=f(x)的圖象有三個不同交點,即方程f(x)=a有三個不同的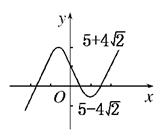 6分
6分
(3) 解:f(x)≥k(x-1),即(x-1)(x2+x-5)≥k(x-1).
因為x>1,所以k≤x2+x-5在(1,+∞)上恒成立.
令g(x)=x2+x-5,此函數在(1,+∞)上是增函數.
所以g(x)>g(1)=-3.
所以k的取值范圍是k≤-3. 10分
考點:導數的運用
點評:本題考查了利用導數求函數單調區間和極值的方法,利用導數研究函數圖象解決根的個數問題的方法,不等式恒成立問題的解法


科目:高中數學 來源: 題型:解答題
某商場銷售某種商品的經驗表明,該商品每日的銷售量y(單位:千克)與銷售價格x(單位:元/千克)滿足關系式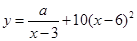 ,其中3<x<6,a 為常數,已知銷售價格為5元/千克時,每日可售出該商品11千克。
,其中3<x<6,a 為常數,已知銷售價格為5元/千克時,每日可售出該商品11千克。
(I)求a的值
(II)若該商品的成品為3元/千克,試確定銷售價格x的值,使商場每日銷售該商品所獲得的利潤最大。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數f(x)=x3-12x+5,x∈R.
(1)求函數f(x)的單調區間和極值;
(2)若關于x的方程f(x)=a有三個不同實根,求實數a的取值范圍;
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數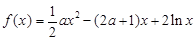 ,其中常數
,其中常數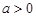 .
.
(1)求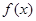 的單調區間;
的單調區間;
(2)如果函數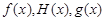 在公共定義域D上,滿足
在公共定義域D上,滿足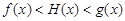 ,那么就稱
,那么就稱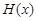 為
為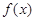 與
與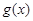 的“和諧函數”.設
的“和諧函數”.設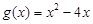 ,求證:當
,求證:當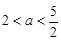 時,在區間
時,在區間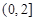 上,函數
上,函數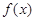 與
與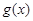 的“和諧函數”有無窮多個.
的“和諧函數”有無窮多個.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com