
 ,則股價
,則股價 (元)和時間
(元)和時間 的關系在
的關系在 段可近似地用解析式
段可近似地用解析式 來描述,從
來描述,從 點走到今天的
點走到今天的 點,是震蕩筑底階段,而今天出現了明顯的筑底結束的標志,且
點,是震蕩筑底階段,而今天出現了明顯的筑底結束的標志,且 點和
點和 點正好關于直線
點正好關于直線 :
: 對稱。老張預計這只股票未來的走勢如圖中虛線所示,這里
對稱。老張預計這只股票未來的走勢如圖中虛線所示,這里 段與
段與 段關于直線
段關于直線 對稱,
對稱, 段是股價延續
段是股價延續 段的趨勢(規律)走到這波上升行
段的趨勢(規律)走到這波上升行
 。現在老張決定取點
。現在老張決定取點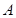
 ,點
,點 ,點
,點 來確定解析式中的常數
來確定解析式中的常數 ,
,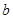 ,
, ,
, ,并且求得
,并且求得 。
。 ,
,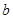 ,
, ,并回答股價什么時候見頂(即求
,并回答股價什么時候見頂(即求 點的橫坐標)
點的橫坐標) 點處的價格買入該股票3000股,到見頂處
點處的價格買入該股票3000股,到見頂處 點的價格全部賣出,不計其它費用,這次操作他能賺多少元?
點的價格全部賣出,不計其它費用,這次操作他能賺多少元?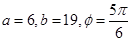 ,當
,當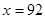 時,股價見頂;(Ⅱ)
時,股價見頂;(Ⅱ)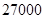 .
. ,
,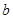 ,
, ,即求
,即求 的解析式,由題意點
的解析式,由題意點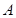
 ,
,  在曲線上,代入解析式,得兩個關系式,由于是三個未知數,還需再找一個條件,注意到
在曲線上,代入解析式,得兩個關系式,由于是三個未知數,還需再找一個條件,注意到 點和
點和 點正好關于直線
點正好關于直線 :
: 對稱,且
對稱,且 點在曲線上,
點在曲線上, ,利用對稱求出
,利用對稱求出 點的坐標為
點的坐標為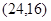 ,代入解析式,又得一個關系式,這樣就可以通過這三個關系式,求出
,代入解析式,又得一個關系式,這樣就可以通過這三個關系式,求出 ,
,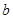 ,
, 的值,并回答股價什么時候見頂(即求
的值,并回答股價什么時候見頂(即求 點的橫坐標),由前面可得在
點的橫坐標),由前面可得在 段的解析式為
段的解析式為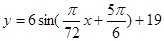 ,利用對稱性得:
,利用對稱性得: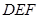 段的解析式為
段的解析式為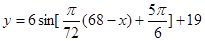 ,利用三角數圖像與性質可得;(Ⅱ)由(Ⅰ)可知,
,利用三角數圖像與性質可得;(Ⅱ)由(Ⅰ)可知,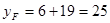 ,由已知
,由已知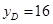 ,算出一股賺
,算出一股賺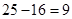 ,故這次操作老張能賺
,故這次操作老張能賺 (元).
(元).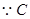 、
、 關于直線
關于直線 對稱
對稱 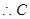 點坐標為
點坐標為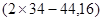 即
即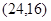
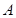 、
、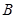 、
、 的坐標代入解析式,得
的坐標代入解析式,得
 ,
,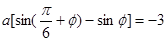 ,③─①得,
,③─①得,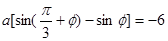 ,
,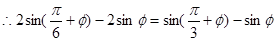 ,
,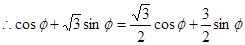 ,
,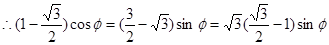 [,,,
[,,,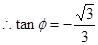 ,
, 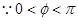 ,
,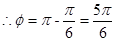 ,代入②,得
,代入②,得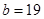 ,再由①得,
,再由①得, ,
, 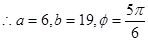 , 7分
, 7分 段的解析式為
段的解析式為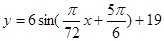 ,由對稱性得:
,由對稱性得: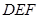 段的解析式為
段的解析式為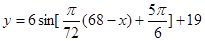 ,
,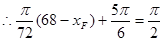 解得
解得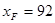 ,
, 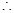 當
當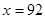 時,股價見頂 10分
時,股價見頂 10分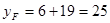 ,故這次操作老張能賺
,故這次操作老張能賺 (元) 12分
(元) 12分

 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 ,
, ,其中實數
,其中實數 .
.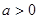 ,求函數
,求函數 的單調區間;
的單調區間; 與
與 的圖象只有一個公共點且
的圖象只有一個公共點且 存在最小值時,記
存在最小值時,記 的最小值為
的最小值為 ,求
,求 的值域;
的值域; 與
與 在區間
在區間 內均為增函數,求實數
內均為增函數,求實數 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
 則下列關于函數
則下列關于函數 的零點個數的判斷正確的是( )
的零點個數的判斷正確的是( )A.當 時,有3個零點;當 時,有3個零點;當 時,有2個零點 時,有2個零點 |
B.當 時,有4個零點;當 時,有4個零點;當 時,有1個零點 時,有1個零點 |
C.無論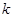 為何值,均有2個零點 為何值,均有2個零點 |
D.無論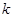 為何值,均有4個零點 為何值,均有4個零點 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
 的定義域為D,若存在閉區間[a,b]
的定義域為D,若存在閉區間[a,b] D,使得函數
D,使得函數 滿足:(1)
滿足:(1) 在[a,b]內是單調函數;(2)
在[a,b]內是單調函數;(2) 在[a,b]上的值域為[2a,2b],則稱區間[a,b]為y=
在[a,b]上的值域為[2a,2b],則稱區間[a,b]為y= 的“美麗區間”.下列函數中存在“美麗區間”的是 . (只需填符合題意的函數序號)
的“美麗區間”.下列函數中存在“美麗區間”的是 . (只需填符合題意的函數序號)  ; ②、
; ②、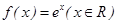 ;
; ; ④、
; ④、 .
.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com