已知

分別是雙曲線

的左、右焦點,過

斜率為

的直線

交雙曲線的左、右兩支分別于

兩點,過

且與

垂直的直線

交雙曲線的左、右兩支分別于
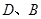
兩點。
(1)求

的取值范圍;
求四邊形

面積的最小值。
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)在四邊形
ABCD中,
BD是它的一條對角線,且
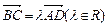
,
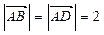
,
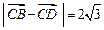
.⑴若△
BCD是直角三形,求
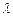
的值;⑵在⑴的條件下,求
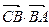
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設
,
是兩個非零向量.則下列命題為真命題的是( )
| A.若|+|=||-||,則⊥ |
| B.若⊥,則|+|=||-|| |
| C.若|+|=||-||,則存在實數(shù)λ,使得=λ |
| D.若存在實數(shù)λ,使得=λ,則|+|=||-|| |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
如圖,
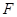
為拋物線
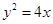
的焦點,A、B、C在拋物線上,若
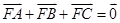
,則
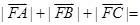
( )
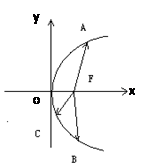
A. 6 B. 4 C. 3 D.2
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)已知
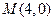
,
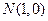
,若動點
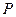
滿足
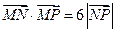
,
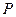
點的軌跡為曲線
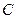
.
(Ⅰ)求曲線
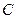
的方程;
(Ⅱ)試確定
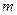
的取值范圍,使得對于直線
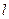
:
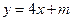
,曲線
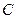
上總有不同的兩點關(guān)于直線
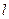
對稱.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知橢圓E:

(




0)過點(0,

),其左焦點

與點P(1,

)的連線與圓

相切。
(1)求橢圓
E的方程;
(2)設
Q為橢圓
E上的一個動點,試判斷以

為直徑的圓與圓

的位置關(guān)系,并證明

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
點B是點A(1,2,3)在坐標平面yOz內(nèi)的射影,則|OB|=
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
15.(幾何證明選講選做題)
如圖3,在

中,

,以

為直徑作半圓交

于

,過

作半圓的切線交

于

,若

,

,則

=
.
查看答案和解析>>

 分別是雙曲線
分別是雙曲線 的左、右焦點,過
的左、右焦點,過 斜率為
斜率為 的直線
的直線 交雙曲線的左、右兩支分別于
交雙曲線的左、右兩支分別于 兩點,過
兩點,過 且與
且與 垂直的直線
垂直的直線 交雙曲線的左、右兩支分別于
交雙曲線的左、右兩支分別于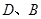 兩點。
兩點。 的取值范圍;
的取值范圍; 面積的最小值。
面積的最小值。 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案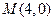 ,
,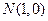 ,若動點
,若動點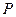 滿足
滿足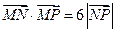 ,
,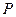 點的軌跡為曲線
點的軌跡為曲線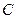 .
.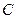 的方程;
的方程;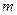 的取值范圍,使得對于直線
的取值范圍,使得對于直線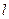 :
: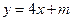 ,曲線
,曲線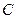 上總有不同的兩點關(guān)于直線
上總有不同的兩點關(guān)于直線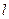 對稱.
對稱. (
(


 0)過點(0,
0)過點(0, ),其左焦點
),其左焦點 與點P(1,
與點P(1, )的連線與圓
)的連線與圓 相切。
相切。 為直徑的圓與圓
為直徑的圓與圓 的位置關(guān)系,并證明
的位置關(guān)系,并證明