在正項數(shù)列
中，
.對任意的
，函數(shù)
滿足
.
（1）求數(shù)列的通項公式；
（2）求數(shù)列
的前
項和
.
（1）
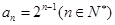；（2）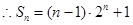
.
解析試題分析：本題主要考查導數(shù)的運算、等比數(shù)列的證明、等比數(shù)列的通項公式、等比數(shù)列的前n項和公式、錯位相減法等基礎知識，考查學生的化歸與轉(zhuǎn)化能力和運算能力.第一問，先利用
得到一個遞推公式，根據(jù)等比數(shù)列的證明方法知數(shù)列為等比數(shù)列，則利用等比數(shù)列的通項公式求基本量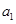
和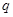
，從而求出通過公式；2.先求出
的表達式，根據(jù)式子的規(guī)律，符合錯位相減法，利用錯位相減法和等比數(shù)列的前n項和求出.
試題解析：（1）求導得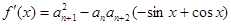
，由可得
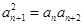，又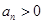
，故數(shù)列為等比數(shù)列，且公比
. 3分
由得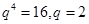
，所以通項公式為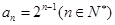. 6分
（2）
①
②
①-②得，
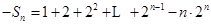
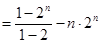
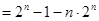
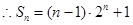12分
考點：導數(shù)的運算、等比數(shù)列的證明、等比數(shù)列的通項公式、等比數(shù)列的前n項和公式、錯位相減法.
科目：高中數(shù)學 來源： 題型：解答題
已知等差數(shù)列{an}的首項a1＝1，公差d>0，且第2項、第5項、第14項分別為等比數(shù)列{bn}的第2項、第3項、第4項．
(1)求數(shù)列{an}，{bn}的通項公式；
(2)設數(shù)列{cn}對n∈N*，均有
＋
＋…＋
＝an＋1成立，求c1＋c2＋c3＋…＋c2014的值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：解答題
設數(shù)列{an}的前n項和為Sn，數(shù)列{Sn}的前n項和為Tn，滿足Tn=2Sn-n2，n∈N﹡.
（1）求a1的值；
（2）求數(shù)列{an}的通項公式.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：解答題
在
個實數(shù)組成的
行列數(shù)表中，先將第一行的所有空格依次填上
，
，
，再將首項為
公比為
的數(shù)列
依次填入第一列的空格內(nèi)，然后按照“任意一格的數(shù)是它上面一格的數(shù)與它左邊一格的數(shù)之和”的規(guī)律填寫其它空格
| | 第1列 | 第2列 | 第3列 | 第4列 | | 第列 |
| 第1行 | | | | | | |
| 第2行 | | | | | | |
| 第3行 |  | | | | | |
| 第4行 |  | | | | | |
 | | | | | | |
| 第行 |  | | | | | |
.試用
表示
的值；
，記為數(shù)列
.的通項
；的值使數(shù)列的前
項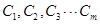
（
）成等比數(shù)列？若能找到，的值是多少？若不能找到，說明理由.查看答案和解析>>
科目：高中數(shù)學 來源： 題型：解答題
已知數(shù)列{an}是等差數(shù)列,數(shù)列{bn}是等比數(shù)列,且對任意的
,都有
.
（1）若{bn }的首項為4,公比為2,求數(shù)列{an+bn}的前n項和Sn;
（2）若
，試探究:數(shù)列{bn}中是否存在某一項,它可以表示為該數(shù)列中其它
項的和？若存在,請求出該項；若不存在,請說明理由．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：解答題
數(shù)列{an}的前n項和記為Sn,a1=t,點(Sn,an+1)在直線y=3x+1上,n∈N*.
(1)當實數(shù)t為何值時,數(shù)列{an}是等比數(shù)列?
(2)在(1)的結(jié)論下,設bn=log4an+1,cn=an+bn,Tn是數(shù)列{cn}的前n項和,求Tn.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：解答題
數(shù)列{an}的前n項和記為Sn，a1＝t，點(Sn，an＋1)在直線y＝2x＋1上，n∈N*.
(1)當實數(shù)t為何值時，數(shù)列{an}是等比數(shù)列？
(2)在(1)的結(jié)論下，設bn＝log3an＋1，Tn是數(shù)列
的前n項和， 求T2 013的值．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
的前
項和
與
滿足
.
的前
.
中，
求數(shù)列
的前n項和Tn．