
設函數
(Ⅰ)當 時,求
時,求 的單調區間;
的單調區間;
(Ⅱ)若當 時,
時, 恒成立,求
恒成立,求 的取值范圍.
的取值范圍.
(1) 的單增區間為
的單增區間為 ,
,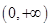 ;單減區間為
;單減區間為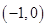 ;(2)
;(2)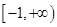 .
.
解析試題分析:本題主要考查導數的運算以及利用導數研究函數的單調性和最值以及恒成立問題,考查函數思想,分類討論思想,考查綜合分析和解決問題的能力.第一問,將 代入得到具體的函數解析式,利用
代入得到具體的函數解析式,利用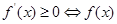 為增函數,
為增函數, 為減函數,解不等式求出函數的單調區間;第二問,化簡
為減函數,解不等式求出函數的單調區間;第二問,化簡 解析式,由于
解析式,由于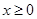 ,所以只需
,所以只需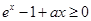 恒成立即可,所以設出新函數
恒成立即可,所以設出新函數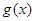 ,求導,判斷
,求導,判斷 的取值范圍,求出函數
的取值范圍,求出函數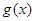 的最小值,令最小值大于等于0,判斷符合題意的
的最小值,令最小值大于等于0,判斷符合題意的 的取值范圍.
的取值范圍.
試題解析:(1)當 時,
時,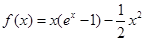 ,
, 2分
2分
令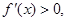 得
得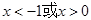 ;令
;令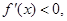 得
得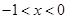
所以 的單增區間為
的單增區間為 ,
,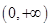 ;單減區間為
;單減區間為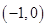 5分
5分
(2)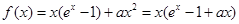 ,令
,令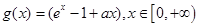 ,
,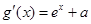 ,
,  7分
7分
當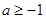 時,
時,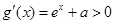 ,
,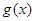 在
在 上為增函數,而
上為增函數,而 ,從而當
,從而當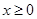 時,
時,
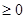 恒成立. 9分
恒成立. 9分
當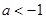 時,令
時,令 ,得
,得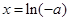 .當
.當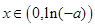 時,
時,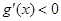 ,
,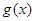 在
在 上是減函數,而
上是減函數,而 ,從而當
,從而當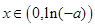 時,
時,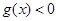 ,即
,即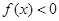
綜上, 的取值范圍是
的取值范圍是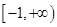 12分
12分
考點:1.利用導數研究函數的單調性;2.恒成立問題;3.利用導數研究函數的最值.


科目:高中數學 來源: 題型:解答題
已知函數f(x)= ax2-(2a+1)x+2ln x,a∈R.
ax2-(2a+1)x+2ln x,a∈R.
(1)若曲線y=f(x)在x=1和x=3處的切線互相平行,求a的值;
(2)求f(x)的單調區間.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數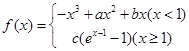 在
在 處存在極值.
處存在極值.
(1)求實數 的值;
的值;
(2)函數 的圖像上存在兩點A,B使得
的圖像上存在兩點A,B使得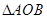 是以坐標原點O為直角頂點的直角三角形,且斜邊AB的中點在
是以坐標原點O為直角頂點的直角三角形,且斜邊AB的中點在 軸上,求實數
軸上,求實數 的取值范圍;
的取值范圍;
(3)當 時,討論關于
時,討論關于 的方程
的方程 的實根個數.
的實根個數.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=(ax2+bx+c)ex且f(0)=1,f(1)=0.
(1)若f(x)在區間[0,1]上單調遞減,求實數a的取值范圍;
(2)當a=0時,是否存在實數m使不等式2f(x)+4xex≥mx+1≥-x2+4x+1對任意x∈R恒成立?若存在,求出m的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數
(1)求 的最小值;
的最小值;
(2)設 ,
, .
.
(ⅰ)證明:當 時,
時, 的圖象與
的圖象與 的圖象有唯一的公共點;
的圖象有唯一的公共點;
(ⅱ)若當 時,
時, 的圖象恒在
的圖象恒在 的圖象的上方,求實數
的圖象的上方,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
經調查統計,某種型號的汽車在勻速行駛中,每小時的耗油量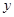 (升)關于行駛速度
(升)關于行駛速度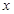 (千米/時)的函數可表示為
(千米/時)的函數可表示為 .已知甲、乙兩地相距
.已知甲、乙兩地相距 千米,在勻速行駛速度不超過
千米,在勻速行駛速度不超過 千米/時的條件下,該種型號的汽車從甲地 到乙地的耗油量記為
千米/時的條件下,該種型號的汽車從甲地 到乙地的耗油量記為 (升).
(升).
(Ⅰ)求函數 的解析式;
的解析式;
(Ⅱ)討論函數 的單調性,當
的單調性,當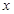 為多少時,耗油量
為多少時,耗油量 為最少?最少為多少升?
為最少?最少為多少升?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com