
已知向量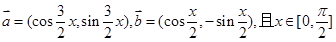 ,
,
(1)求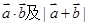 ;
;
(2)若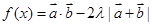 的最小值是
的最小值是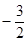 ,求實(shí)數(shù)
,求實(shí)數(shù)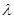 的值.
的值.
(1)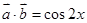 ,
,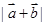 =2cosx(2)
=2cosx(2)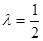
解析試題分析:(1)由向量的坐標(biāo)運(yùn)算,利用公式化簡(jiǎn)即可;(2)原函數(shù)由向量坐標(biāo)運(yùn)算可化為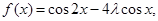 即
即 又最小值
又最小值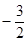 ,則結(jié)合二次函數(shù)最值可求得
,則結(jié)合二次函數(shù)最值可求得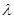 .
.
試題解析:解:(1) =
=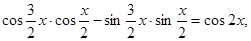
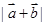 =
=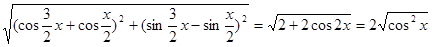 ,
,
∵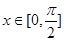 ,∴
,∴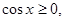
∴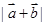 =2cosx. 6分
=2cosx. 6分
(2)由(1)得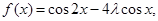
即
∵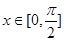 ,∴
,∴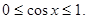
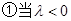 時(shí),當(dāng)且僅當(dāng)
時(shí),當(dāng)且僅當(dāng)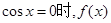 取得最小值-1,這與已知矛盾.
取得最小值-1,這與已知矛盾.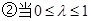 時(shí),當(dāng)且僅當(dāng)
時(shí),當(dāng)且僅當(dāng)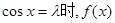 取最小值
取最小值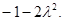
由已知得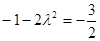 ,解得
,解得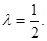
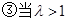 時(shí),當(dāng)且僅當(dāng)
時(shí),當(dāng)且僅當(dāng)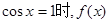 取得最小值
取得最小值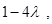
由已知得 ,解得
,解得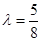 ,這與
,這與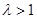 相矛盾.
相矛盾.
綜上所述,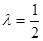 為所求. 12分
為所求. 12分
考點(diǎn):向量的坐標(biāo)運(yùn)算,二次函數(shù)求最值,函數(shù)與方程的數(shù)學(xué)思想,分類討論的數(shù)學(xué)思想.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知向量a=(cosθ,sinθ),θ∈[0,π],向量b=(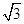 ,-1).
,-1).
(1)若a⊥b,求θ的值;
(2)若|2a-b|<m恒成立,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知向量a=(1,2),b=(2,-2).
(1)設(shè)c=4a+b,求(b·c)a;
(2)若a+λb與a垂直,求λ的值;
(3)求向量a在b方向上的投影.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本題滿分12分)本題共有2個(gè)小題,第1小題滿分4分,第2個(gè)小題滿分8分。
已知復(fù)數(shù)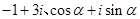 (
(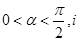 是虛數(shù)單位)在復(fù)平面上對(duì)應(yīng)的點(diǎn)依次為
是虛數(shù)單位)在復(fù)平面上對(duì)應(yīng)的點(diǎn)依次為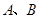 ,點(diǎn)
,點(diǎn)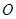 是坐標(biāo)原點(diǎn).
是坐標(biāo)原點(diǎn).
(1)若 ,求
,求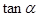 的值;
的值;
(2)若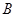 點(diǎn)的橫坐標(biāo)為
點(diǎn)的橫坐標(biāo)為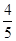 ,求
,求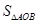 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
在四邊形ABCD中 , ,
, ,
, ,其中
,其中
(1)若 ,試求
,試求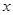 與
與 之間的表達(dá)式;
之間的表達(dá)式;
(2)在(1)的條件下,若又有 ,試求
,試求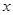 、
、 的值及四邊形
的值及四邊形 的面積。
的面積。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知向量a="(cos" α,sin α),b="(cos" β,sin β),0<β<α<π.
(1)若|a-b|=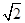 ,求證:a⊥b;
,求證:a⊥b;
(2)設(shè)c=(0,1),若a+b=c,求α,β的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
設(shè)兩向量e1、e2滿足|e1|=2,|e2|=1,e1、e2的夾角為60°,若向量2te1+7e2與向量e1+te2的夾角為鈍角,求實(shí)數(shù)t的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:單選題
[2013·江西撫州月考]數(shù)列{an}的前n項(xiàng)積為n2,那么當(dāng)n≥2時(shí),{an}的通項(xiàng)公式為( )
| A.a(chǎn)n=2n-1 | B.a(chǎn)n=n2 |
C.a(chǎn)n= | D.a(chǎn)n= |
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com