
(本題滿分12分)本題共有2個小題,第1小題滿分4分,第2個小題滿分8分。
已知復數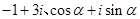 (
(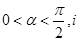 是虛數單位)在復平面上對應的點依次為
是虛數單位)在復平面上對應的點依次為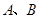 ,點
,點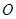 是坐標原點.
是坐標原點.
(1)若 ,求
,求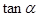 的值;
的值;
(2)若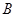 點的橫坐標為
點的橫坐標為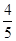 ,求
,求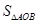 .
.
(1)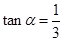 ,(2)
,(2)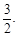
解析試題分析:(1)根據復數與平面上點一一對應關系有: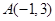 ,
,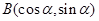 ,從而
,從而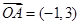 ,
,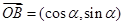 ,由
,由 得
得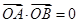 ∴
∴ ,
,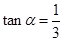 ,(2)由⑴
,(2)由⑴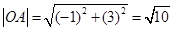 , 記
, 記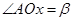 ,
, 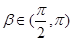 ∴
∴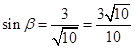 ,
,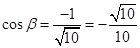 ,
,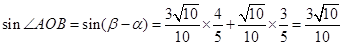 ∴
∴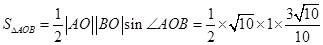
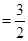
試題解析:⑴解法1:由題可知: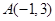 ,
,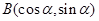 ,
,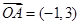 ,
,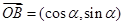 2分
2分 ,得
,得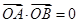 ∴
∴ ,
,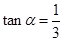 4分
4分
解法2:由題可知: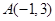 ,
,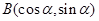 ,
,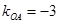 ,
, 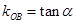 2分
2分
∵ ,∴
,∴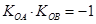
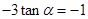 , 得
, 得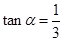 4分
4分
(2)解法1:由⑴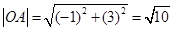 , 記
, 記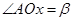 ,
, 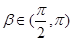
∴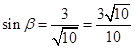 ,
,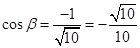 (每式1分) 6分
(每式1分) 6分
∵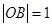
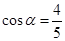 ,得
,得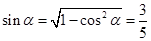 (列式計算各1分) 8分
(列式計算各1分) 8分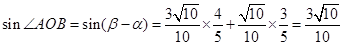 (列式計算各1分)10分
(列式計算各1分)10分
∴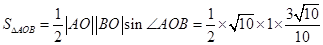
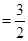 (列式計算各1分)12分
(列式計算各1分)12分
解法2:由題意得: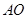 的直線方程為
的直線方程為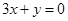 6分
6分
則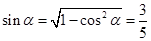 即
即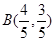 (列式計算各1分) 8分
(列式計算各1分) 8分
則點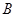 到直線
到直線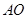 的距離為
的距離為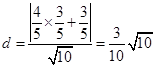 (列式計算各1分) 10分
(列式計算各1分) 10分
又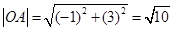 ,∴
,∴ 12分
12分
解法3: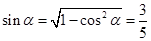 即
即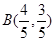 (每式1分) 6分
(每式1分) 6分
即: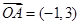 ,
,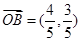 7分
7分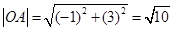 ,
,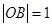 ,
,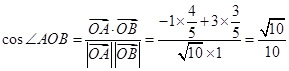 9分
9分
∴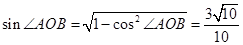 10分
10分
則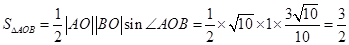 (列式計算各1分)12分
(列式計算各1分)12分
考點:向量垂直坐標表示,兩角差正弦公式


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:高中數學 來源: 題型:解答題
已知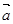 =(
=(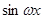 ,
,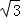
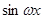 ),
), =(
=(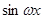 ,
,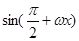 ),(ω>0),
),(ω>0),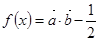 且
且 的最小正周期是
的最小正周期是 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若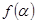 =
=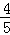 (
(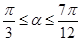 ),求
),求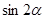 值;
值;
(Ⅲ)若函數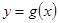 與
與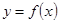 的圖象關于直線
的圖象關于直線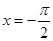 對稱,且方程
對稱,且方程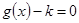 在區間
在區間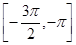 上有解,求
上有解,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(2014·長春模擬)已知向量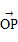 =
=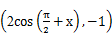 ,
,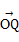 =
=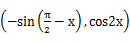 ,定義函數f(x)=
,定義函數f(x)=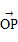 ·
·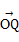 .
.
(1)求函數f(x)的表達式,并指出其最大值和最小值.
(2)在銳角△ABC中,角A,B,C的對邊分別為a,b,c,且f(A)=1,bc=8,求△ABC的面積S.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知點A(2,3),B(5,4),C(7,10),若 =
= +λ·
+λ· (λ∈R),試問:
(λ∈R),試問:
(1) λ為何值時,點P在第一、三象限角平分線上;
(2) λ為何值時,點P在第三象限.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com