
已知函數(shù)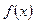 的定義域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/c8/d/1sm544.gif" style="vertical-align:middle;" />,且滿足條件:①
的定義域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/c8/d/1sm544.gif" style="vertical-align:middle;" />,且滿足條件:①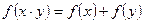 ,②
,②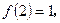 ③當(dāng)
③當(dāng)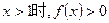 .
.
(1)求證:函數(shù)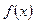 為偶函數(shù);
為偶函數(shù);
(2)討論函數(shù)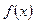 的單調(diào)性;
的單調(diào)性;
(3)求不等式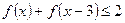 的解集
的解集
解:(1)在①中令x="y=1," 得f(1)= f(1)+ f(1)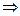 f(1)=0,
f(1)=0,
令x=y=-1, 得f(1)= f(-1 )+ f(-1)
)+ f(-1)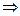 f(-1)=0,
f(-1)=0,
再令y=-1, 得f(-x)= f(x)+ f(-1)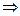 f(x), ∴f(x)為偶函 數(shù);
f(x), ∴f(x)為偶函 數(shù);
(2)在①中令
先討論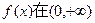 上的單調(diào)性, 任取x1http://www.zxxk.com/x2,設(shè)x2>x1>0,
上的單調(diào)性, 任取x1http://www.zxxk.com/x2,設(shè)x2>x1>0,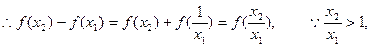
由③知: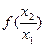 >0,∴f(x2)>f(x1), ∴f(x)在(0,+∞)上是增函數(shù),
>0,∴f(x2)>f(x1), ∴f(x)在(0,+∞)上是增函數(shù),
∵偶函數(shù)圖象關(guān)于y軸對稱 ,∴f(x)在(-∞,0)上是減函數(shù);[來源:Z+xx+k.Com]
(3)∵f[x(x-3)]= f(x)+ f(x-3)≤2, 由①②得2=1+1= f(2)+ f(2)= f( 4)= f(-4),
4)= f(-4),
1)若x(x-3)>0 , ∵f(x)在(0,+∞)上為 增函數(shù),
增函數(shù),
由f[x(x-3)] ≤f(4) 得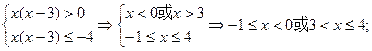
2)若x(x-3)<0 , ∵f(x)在(-∞,0)上為減函數(shù);
, ∵f(x)在(-∞,0)上為減函數(shù);
由f[x(x-3)] ≤f(-4)得 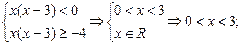
∴原不等式的解集為: 
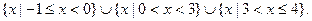
解析



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)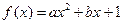 (
( 為實(shí)數(shù),
為實(shí)數(shù), ,
,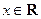 ).
).
(1)當(dāng)函數(shù) 的圖像過點(diǎn)
的圖像過點(diǎn)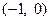 ,且方程
,且方程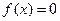 有且只有一個根,求
有且只有一個根,求 的表達(dá)式;
的表達(dá)式;
(2)若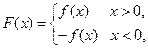 當(dāng)
當(dāng)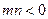 ,
,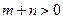 ,
,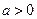 ,且函數(shù)
,且函數(shù) 為偶函數(shù)時,試判斷
為偶函數(shù)時,試判斷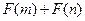 能否大于
能否大于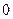 ?
?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
某自來水廠的蓄水池中有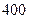 噸水,每天零點(diǎn)開始向居民供水,同時以每小時
噸水,每天零點(diǎn)開始向居民供水,同時以每小時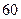 噸的速度向池中注水.已知
噸的速度向池中注水.已知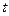 小時內(nèi)向居民供水總量為
小時內(nèi)向居民供水總量為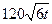 噸
噸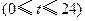 ,問
,問
(1)每天幾點(diǎn)時蓄水池中的存水量最少?
(2)若池中存水量不多于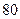 噸時,就會出現(xiàn)供水緊張現(xiàn)象,則每天會有幾個小時出現(xiàn)這種現(xiàn)象?
噸時,就會出現(xiàn)供水緊張現(xiàn)象,則每天會有幾個小時出現(xiàn)這種現(xiàn)象?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(12分 ) .已知函數(shù)y=
) .已知函數(shù)y= f(x)=
f(x)=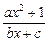 (a,b,c∈R,a>0,b>0)是奇函數(shù),當(dāng)x>0時,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函數(shù),當(dāng)x>0時,f(x)有最小值2,其中b∈N且f(1)<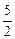
(1)試求函數(shù)f(x)的解析式
(2)問函數(shù)f(x)圖象上是否存在關(guān)于點(diǎn)(1,0)對稱的兩點(diǎn),若存在,求出點(diǎn)的坐標(biāo);若不存在,說 明理由.
明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)
(文科)已知二次函數(shù)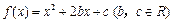 ,且
,且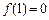 .
.
(1)若函數(shù)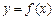 與x軸的兩個交點(diǎn)
與x軸的兩個交點(diǎn)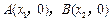 之間的距離為2,求b的值;
之間的距離為2,求b的值;
(2)若關(guān)于x的方程 的兩個實(shí)數(shù)根分別在區(qū)間
的兩個實(shí)數(shù)根分別在區(qū)間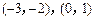 內(nèi),求b的取值范圍.
內(nèi),求b的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
某微機(jī)培訓(xùn)機(jī)構(gòu)打算購進(jìn)一批微機(jī)桌和鼠標(biāo)墊 ,市場價微機(jī)桌每張為150元,鼠標(biāo)墊每個為5元,該培訓(xùn)機(jī)構(gòu)老板聯(lián)系了兩家商場甲和乙,由于用貨量大,這
,市場價微機(jī)桌每張為150元,鼠標(biāo)墊每個為5元,該培訓(xùn)機(jī)構(gòu)老板聯(lián)系了兩家商場甲和乙,由于用貨量大,這 兩家商場都給出了優(yōu)惠條件
兩家商場都給出了優(yōu)惠條件
商場甲:買一贈一,買一張微機(jī)桌,贈一個鼠標(biāo)墊
商場乙:打折,按總價的95%收款
該培訓(xùn)機(jī)構(gòu)需要微機(jī)桌 60張,鼠標(biāo)墊
60張,鼠標(biāo)墊 個(
個(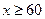 ),如果兩種商品只能在一家購買,請你幫助該培訓(xùn)機(jī)構(gòu)老板選擇在哪一家商場買更省錢?
),如果兩種商品只能在一家購買,請你幫助該培訓(xùn)機(jī)構(gòu)老板選擇在哪一家商場買更省錢?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com