知圓
C1的方程為(
x-2)
2+(
y-1)
2=

,橢圓
C2的方程為

=1(
a>
b>0),
C2的離心率為
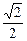
,如果
C1與
C2相交于
A、
B兩點,且線段
AB恰為圓
C1的直徑,求直線
AB的方程和橢圓
C2的方程.

橢圓方程為
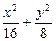
=1.
由
e=
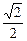
,可設(shè)橢圓方程為
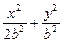
=1,
又設(shè)
A(
x1,
y1)、
B(
x2,
y2),則
x1+
x2=4,
y1+
y2=2,
又
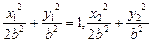
=1,兩式相減,得
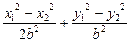
=0,
即(
x1+
x2)(
x1-
x2)+2(
y1+
y2)(
y1-
y2)=0.
化簡得
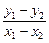
=-1,故直線
AB的方程為
y=-
x+3,
代入橢圓方程得3
x2-12
x+18-2
b2=0.
有
Δ=24
b2-72>0,又|
AB|=
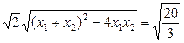
,
得
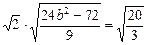
,解得
b2=8.
故所求橢圓方程為
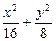
=1.
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:單選題
圓
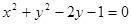
關(guān)于直線
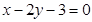
對稱的圓方程是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
把直線
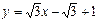
繞點(1,1)順時針旋轉(zhuǎn),使它與圓
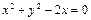
相切,則直線轉(zhuǎn)動的最小正角是
。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
與圓x
2+y
2-4x+2y+4=0關(guān)于直線x-y+3=0成軸對稱的圓的方程是( )
| A.x2+y2-8x+10y+40=0 |
| B.x2+y2-8x+10y+20=0 |
| C.x2+y2+8x-10y+40=0 |
| D.x2+y2+8x-10y+20=0 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
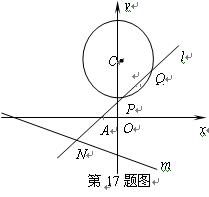
已知過點
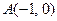
的動直線
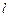
與圓
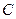
:
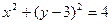
相交于
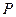
、
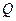
兩點,

與
直線
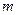
:
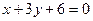
相交于
.
(1)求證:當

與
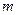
垂直時,

必過圓心
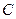
;
(2)當
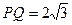
時,求直線

的方程.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
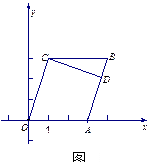
(2)過點
C做
CD⊥
AB于點
D,求
CD所在直線的方程.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知圓方程:

,求圓心到直線

的距離的取值范圍.(14分)
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
點M(x
0,y
0)是圓x
2+y
2=a
2(a>0)內(nèi)不為圓心的一點,則直線x
0x+y
0y=a
2與該圓的位置關(guān)系是
( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
點
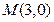
是圓
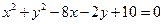
內(nèi)一點,過
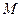
點最長的弦所在的直線的
方程為( ).
查看答案和解析>>

 ,橢圓C2的方程為
,橢圓C2的方程為 =1(a>b>0),C2的離心率為
=1(a>b>0),C2的離心率為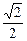 ,如果C1與C2相交于A、B兩點,且線段AB恰為圓C1的直徑,求直線AB的方程和橢圓C2的方程.
,如果C1與C2相交于A、B兩點,且線段AB恰為圓C1的直徑,求直線AB的方程和橢圓C2的方程.
 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案