
已知長(zhǎng)方體ABCD—A1B1ClD1內(nèi)接于球O,底面ABCD是邊長(zhǎng)為2的正方形,E為AA1的中點(diǎn),OA⊥平面BDE,則球O的表面積為
A.8 | B.16 : : | C.14 | D.18 |
B.
解析試題分析:∵長(zhǎng)方體ABCD—A1B1ClD1內(nèi)接于球O,∴球心O是A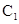 中點(diǎn)。
中點(diǎn)。
∵ABCD是邊長(zhǎng)為2的正方形,∴BD=2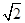 ,
,
設(shè)BD中點(diǎn)為O‘,連接OO'
∴OO'⊥平面ABCD
∵E為A 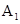 的中點(diǎn),
的中點(diǎn),
∴AE//OO', AE=OO'
∴AO'OE為矩形
∵OA垂直平面BDE
∴OA⊥EO'
∴AO'OE為正方形
∴AO=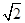 AO'=2
AO'=2
即球O的半徑R=2
∴球O面積4πR²=16π,故選B。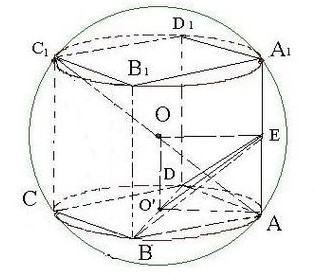
考點(diǎn):本題主要考查立體幾何平行關(guān)系、垂直關(guān)系、長(zhǎng)方體、球的幾何特征,球的表面積計(jì)算。
點(diǎn)評(píng):中檔題,首先認(rèn)定球心O是A 中點(diǎn),圍繞球半徑的計(jì)算,構(gòu)造出現(xiàn)直角三角形,利用直角三角形的邊角關(guān)系求解。
中點(diǎn),圍繞球半徑的計(jì)算,構(gòu)造出現(xiàn)直角三角形,利用直角三角形的邊角關(guān)系求解。


 奪冠訓(xùn)練單元期末沖刺100分系列答案
奪冠訓(xùn)練單元期末沖刺100分系列答案 新思維小冠軍100分作業(yè)本系列答案
新思維小冠軍100分作業(yè)本系列答案 名師指導(dǎo)一卷通系列答案
名師指導(dǎo)一卷通系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:單選題
已知ABCD是矩形,邊長(zhǎng)AB=3,BC=4,正方形ACEF邊長(zhǎng)為5,平面ACEF⊥平面ABCD,則多面體ABCDEF的外接球的表面積 ( )
A.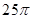 | B.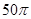 | C.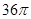 | D.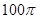 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:單選題
若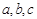 是空間三條不同的直線,
是空間三條不同的直線,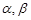 是空間兩個(gè)不同的平面,則下列命題中,逆命題不正確的是( )
是空間兩個(gè)不同的平面,則下列命題中,逆命題不正確的是( )
A.當(dāng)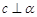 時(shí),若 時(shí),若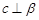 ,則 ,則 |
B.當(dāng)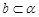 時(shí),若 時(shí),若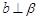 ,則 ,則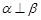 |
C.當(dāng)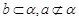 且 且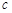 是 是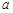 在 在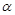 內(nèi)的射影時(shí),若 內(nèi)的射影時(shí),若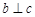 ,則 ,則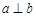 |
D.當(dāng)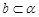 且 且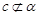 時(shí),若 時(shí),若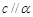 ,則 ,則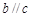 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:單選題
如圖所示,點(diǎn)P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,則PB與AC所成的角是( )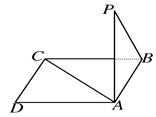
| A.90° | B.60° |
| C.45° | D.30° |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:單選題
如圖,在直棱柱ABC—A1B1C1中,AC=BC=2,∠ACB=90º,AA1=2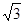 ,E,F(xiàn)分別為AB、CB中點(diǎn),過(guò)直線EF作棱柱的截面,若截面與平面ABC所成的二面角的大小為60º,則截面的面積為( ).
,E,F(xiàn)分別為AB、CB中點(diǎn),過(guò)直線EF作棱柱的截面,若截面與平面ABC所成的二面角的大小為60º,則截面的面積為( ).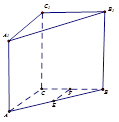
A.3或1 B.1 C.4或1 D.3或4
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:單選題
已知 是平面,
是平面,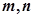 是直線,給出下列命題,其中正確的命題的個(gè)數(shù)是( )
是直線,給出下列命題,其中正確的命題的個(gè)數(shù)是( )
( 1 )若 ,則
,則
( 2 )若 ,則
,則
( 3 )如果 是異面直線,那么
是異面直線,那么 與
與 相交
相交
( 4 )若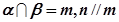 ,且
,且 ,則
,則 且
且 .
.
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com