
已知奇函數(shù) f (x) 在 (-¥,0)∪(0,+¥) 上有意義,且在 (0,+¥) 上是增函數(shù),f (1) = 0,又函數(shù) g(q) = sin 2q+ m cos q-2m,若集合M =" {m" | g(q) < 0},集合 N =" {m" | f [g(q)] < 0},求M∩N.
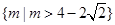 .
.
解析試題分析:根據(jù)條件中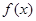 是奇函數(shù)的這一條件可以求得使
是奇函數(shù)的這一條件可以求得使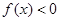 的
的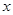 的范圍,再根據(jù)
的范圍,再根據(jù)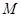 與
與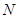 的表達(dá)式,可以得到
的表達(dá)式,可以得到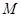 與
與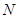 的交集即是使
的交集即是使 恒成立的所有
恒成立的所有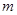 的全體,通過參變分離可以將問題轉(zhuǎn)化為求使
的全體,通過參變分離可以將問題轉(zhuǎn)化為求使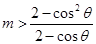 恒成立的
恒成立的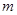 的取值范圍,通過求函數(shù)最大值,進(jìn)而可以求出
的取值范圍,通過求函數(shù)最大值,進(jìn)而可以求出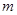 的范圍.
的范圍.
依題意,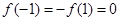 ,又
,又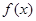 在
在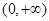 上是增函數(shù),
上是增函數(shù),
∴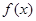 在
在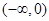 上也是增函數(shù), 1分
上也是增函數(shù), 1分
∴ 由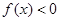 得
得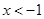 或
或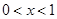 2分
2分
∴ 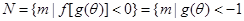 或
或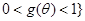 3分
3分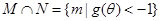 4分
4分
由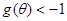 得
得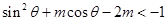 5分
5分
即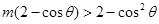 6分
6分
∴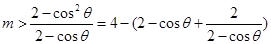 7分
7分
設(shè)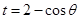 ,
,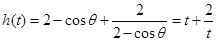 9分
9分
∵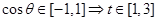 , 10分
, 10分
∴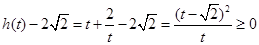 , 11分
, 11分
且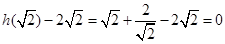 12分
12分
∴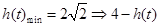 的最大值為
的最大值為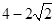 13分
13分
∴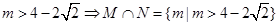 14分
14分
另解:本題也可用下面解法:
1. 用單調(diào)性定義證明單調(diào)性
∵對任意 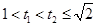 ,
,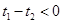 ,
,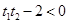 ,
,
∴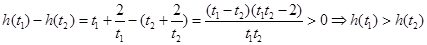 ,
,
即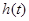 在
在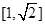 上為減函數(shù),
上為減函數(shù),
同理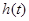 在
在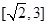 上為增函數(shù),得
上為增函數(shù),得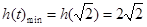 5分
5分
∴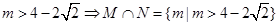 .
.
2. 二次函數(shù)最值討論
解:依題意,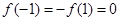 ,又
,又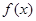 在
在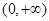 上是增函數(shù),
上是增函數(shù),
∴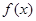 在
在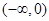



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知定義在R上的奇函數(shù) 有最小正周期2,且當(dāng)
有最小正周期2,且當(dāng)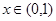 時(shí),
時(shí), .
.
(1)求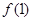 和
和 的值;
的值;
(2)求 在[-1,1]上的解析式.
在[-1,1]上的解析式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)f(x)=|ax-2|+bln x(x>0,實(shí)數(shù)a,b為常數(shù)).
(1)若a=1,f(x)在(0,+∞)上是單調(diào)增函數(shù),求b的取值范圍;
(2)若a≥2,b=1,求方程f(x)= 在(0,1]上解的個(gè)數(shù).
在(0,1]上解的個(gè)數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,經(jīng)過村莊A有兩條夾角為60°的公路AB,AC,根據(jù)規(guī)劃擬在兩條公路之間的區(qū)域內(nèi)建一工廠P,分別在兩條公路邊上建兩個(gè)倉庫M、N (異于村莊A),要求PM=PN=MN=2(單位:千米).如何設(shè)計(jì), 可以使得工廠產(chǎn)生的噪聲對居民的影響最小(即工廠與村莊的距離最遠(yuǎn)).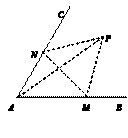
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
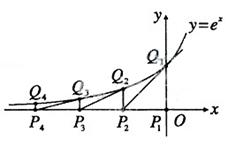
如圖,從點(diǎn)P1(0,0)作 軸的垂線交曲線
軸的垂線交曲線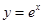 于點(diǎn)
于點(diǎn)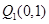 ,曲線在
,曲線在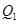 點(diǎn)處的切線與
點(diǎn)處的切線與 軸交于點(diǎn)
軸交于點(diǎn)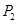 .再從
.再從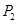 做
做 軸的垂線交曲線于點(diǎn)
軸的垂線交曲線于點(diǎn)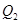 ,依次重復(fù)上述過程得到一系列點(diǎn):
,依次重復(fù)上述過程得到一系列點(diǎn):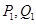 ;
;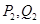 ;…;
;…; ,記
,記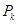 點(diǎn)的坐標(biāo)為
點(diǎn)的坐標(biāo)為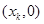 (
(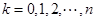 ).
).
(1)試求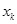 與
與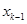 的關(guān)系(
的關(guān)系(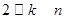 );
);
(2)求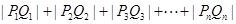 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,某機(jī)場建在一個(gè)海灣的半島上,飛機(jī)跑道AB的長為4.5km,且跑道所在的直線與海岸線l的夾角為60o(海岸線可以看作是直線),跑道上離海岸線距離最近的點(diǎn)B到海岸線的距離BC=4 km.D為海灣一側(cè)海岸線CT上的一點(diǎn),設(shè)CD=x(km),點(diǎn)D對跑道AB的視角為q.
km.D為海灣一側(cè)海岸線CT上的一點(diǎn),設(shè)CD=x(km),點(diǎn)D對跑道AB的視角為q.
(1)將tanq表示為x的函數(shù);
(2)求點(diǎn)D的位置,使q取得最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)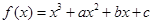 在
在 與
與 時(shí)都取得極值.
時(shí)都取得極值.
(1)求 的值與函數(shù)
的值與函數(shù) 的單調(diào)區(qū)間
的單調(diào)區(qū)間
(2)若對 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com