Question

若公比為c的等比數(shù)列{a_n}的首項(xiàng)a₁=1且滿足a_n=(n=3,4,…).

(1)求c的值;

(2)求數(shù)列{na_n}的前n項(xiàng)和S_n.

Answer 1

解：(1)由題設(shè),當(dāng)n≥3時(shí),a_n=c²a_n-2,

a_n-1=ca_n-2,

a_n=

由題設(shè)條件可得:a_n-2≠0,因此c²=,即

2c²-c-1=0.

解得c=1或c=.

(2)由(1)知需要分兩種情況討論.

當(dāng)c=1時(shí),數(shù)列{a_n}是一個(gè)常數(shù)列,

即a_n=1(n∈N₊).

這時(shí),數(shù)列{na_n}的前n項(xiàng)和

S_n=1+2+3+…+n=.

當(dāng)c=時(shí),數(shù)列{a_n}是一個(gè)公比為的等比數(shù)列,即a_n=()^n-1(n∈N₊).

這時(shí),數(shù)列{na_n}的前n項(xiàng)和

S_n=1+2×()+3×()²+…+n·()^n-1,               ①

①式兩邊同乘,得S_n=+2×()²+…+(n-1)·()^n-1+n·()ⁿ.         ②

①式減去②式,得

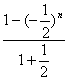(1+)S_n=1+()+()²+…+()^n-1-n·()ⁿ=-n()ⁿ.

所以S_n=［4-(-1)ⁿ］(n∈N₊).

溫馨提示

    （1）對(duì)于等比數(shù)列的判定，往往由通項(xiàng)公式?jīng)Q定，同時(shí)本題更用到了等比數(shù)列前n項(xiàng)和S_n的推導(dǎo)方法——錯(cuò)位相減法.

    (2)一般地，如果數(shù)列{a_n}是等差數(shù)列，{b_n}是等比數(shù)列，公比為q，求數(shù)列{a_n·b_n}的前n項(xiàng)和時(shí)，可采用這一思路和方法.

    (3)在寫出“S_n”與“qS_n”的表達(dá)式時(shí)應(yīng)特別注意將兩式“錯(cuò)項(xiàng)對(duì)齊”，以便于下一步準(zhǔn)確寫出“S_n-qS_n”的表達(dá)式.