
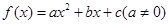 滿足條件:①當
滿足條件:①當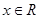 時,
時,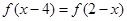 ,且
,且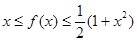 ;②
;② 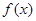 在
在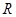 上的最小值為
上的最小值為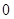 。(1)求
。(1)求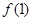 的值及
的值及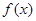 的解析式;(2)若
的解析式;(2)若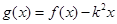 在
在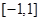 上是單調函數,求
上是單調函數,求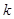 的取值范圍;(3)求最大值
的取值范圍;(3)求最大值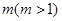 ,使得存在
,使得存在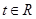 ,只要
,只要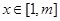 ,就有
,就有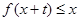 。
。 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案科目:高中數學 來源:不詳 題型:解答題
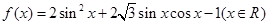 .
.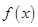 的圖像是由函數
的圖像是由函數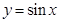 的圖像經過怎樣的變換得到的;
的圖像經過怎樣的變換得到的;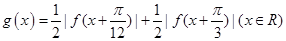 ,試判斷函數
,試判斷函數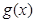 的奇偶性,并用反證法證明函數
的奇偶性,并用反證法證明函數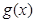 的最小正周期是
的最小正周期是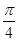 ;
;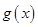 的單調區間和值域.
的單調區間和值域.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
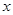 (百萬元)請李子恒老師進行創作,經調研知:該唱片的總利潤
(百萬元)請李子恒老師進行創作,經調研知:該唱片的總利潤 (百萬元)與
(百萬元)與 成正比的關系,當
成正比的關系,當 時
時 .又有
.又有 ,其中
,其中 是常數,且
是常數,且 .
. ,求其表達式,定義域(用
,求其表達式,定義域(用 表示);
表示); 的最大值及相應的
的最大值及相應的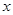 的值.
的值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com