
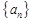 的前
的前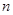 項和為
項和為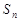 (
(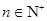 ), 關于數列
), 關于數列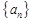 有下列三個命題:
有下列三個命題: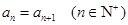 ,則
,則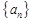 既是等差數列又是等比數列;
既是等差數列又是等比數列;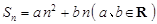 ,則
,則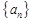 是等差數列;
是等差數列;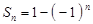 ,則
,則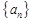 是等比數列。
是等比數列。 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:不詳 題型:解答題
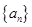 是等差數列,且
是等差數列,且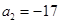 ,
,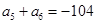 ;又若
;又若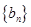 是各項為正數的等比數列,且滿足
是各項為正數的等比數列,且滿足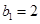 ,其前
,其前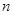 項和為
項和為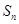 ,
,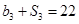 .
.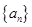 ,
,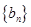 的通項公式
的通項公式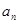 ,
,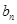 ;
;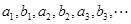 的前
的前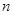 項和為
項和為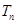 ,求
,求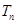 的表達式,并求
的表達式,并求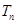 的最小值.
的最小值.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
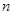 年該生產線設備低劣化值為
年該生產線設備低劣化值為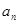 ,求
,求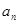 的表達式;
的表達式;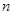 年設備低劣化平均值為
年設備低劣化平均值為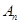 ,當
,當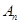 達到或超過12萬元時,則當年需要更新生產線,試判斷第幾年需要更新該生產線,并說明理由.
達到或超過12萬元時,則當年需要更新生產線,試判斷第幾年需要更新該生產線,并說明理由.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
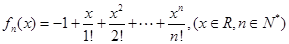
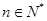 ,存在唯一的
,存在唯一的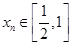 ,滿足
,滿足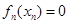 ;
;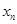 構成數列
構成數列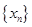 ,判斷數列
,判斷數列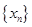 的單調性并證明;
的單調性并證明;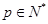 ,
,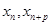 滿足(Ⅰ),試比較
滿足(Ⅰ),試比較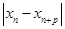 與
與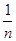 的大小.
的大小.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com