
已知向量a= ,b=
,b= ,且x∈
,且x∈ .
.
(1)求a·b及|a+b|;
(2)若f(x)=a·b-2λ|a+b|的最小值為- ,求正實數(shù)λ的值.
,求正實數(shù)λ的值.
 小天才課時作業(yè)系列答案
小天才課時作業(yè)系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優(yōu)好卷系列答案
陽光同學一線名師全優(yōu)好卷系列答案科目:高中數(shù)學 來源: 題型:解答題
已知關(guān)于x的方程:x2-(6+i)x+9+ai=0(a∈R)有實數(shù)根b.
(1)求實數(shù)a,b的值.
(2)若復數(shù)滿足|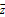 -a-bi|-2|z|=0,求z為何值時,|z|有最小值,并求出|z|的最小值.
-a-bi|-2|z|=0,求z為何值時,|z|有最小值,并求出|z|的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知四點A(x,0),B(2x,1),C(2,x),D(6,2x).
(1)求實數(shù)x,使兩向量 ,
, 共線.
共線.
(2)當兩向量 與
與 共線時,A,B,C,D四點是否在同一條直線上?
共線時,A,B,C,D四點是否在同一條直線上?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
如圖,設(shè) 是單位圓上一點,一個動點從點
是單位圓上一點,一個動點從點 出發(fā),沿圓周按逆時針方向勻速旋轉(zhuǎn),12秒旋轉(zhuǎn)一周.
出發(fā),沿圓周按逆時針方向勻速旋轉(zhuǎn),12秒旋轉(zhuǎn)一周. 秒時,動點到達點
秒時,動點到達點 ,
, 秒時動點到達點
秒時動點到達點 .設(shè)
.設(shè) ,其縱坐標滿足
,其縱坐標滿足 .
.
(1)求點 的坐標,并求
的坐標,并求 ;
;
(2)若 ,求
,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
設(shè) 為拋物線
為拋物線 (
( )的焦點,
)的焦點,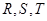 為該拋物線上三點,若
為該拋物線上三點,若 ,且
,且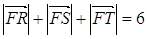
(Ⅰ)求拋物線 的方程;
的方程;
(Ⅱ) 點的坐標為(
點的坐標為(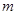 ,
, )其中
)其中 ,過點F作斜率為
,過點F作斜率為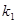 的直線與拋物線交于
的直線與拋物線交于 、
、 兩點,
兩點, 、
、 兩點的橫坐標均不為
兩點的橫坐標均不為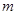 ,連結(jié)
,連結(jié) 、
、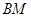 并延長交拋物線于
并延長交拋物線于 、
、 兩點,設(shè)直線
兩點,設(shè)直線 的斜率為
的斜率為 .若
.若 ,求
,求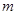 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:單選題
兩千多年前,古希臘畢達哥拉斯學派的數(shù)學家曾經(jīng)在沙灘上研究數(shù)學問題.他們在沙灘上畫點或用小石子表示數(shù),按照點或小石子能排列的形狀對數(shù)進行分類.如下圖中實心點的個數(shù) ,
, ,
, ,
, ,…為梯形數(shù).根據(jù)圖形的構(gòu)成,記此數(shù)列的第
,…為梯形數(shù).根據(jù)圖形的構(gòu)成,記此數(shù)列的第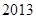 項為
項為 ,則
,則 ( )
( )
A. | B. | C. | D. |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
設(shè)兩向量e1、e2滿足|e1|=2,|e2|=1,e1、e2的夾角為60°,若向量2te1+7e2與向量e1+te2的夾角為鈍角,求實數(shù)t的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com