
如圖,有一塊正方形區域ABCD,現在要劃出一個直角三角形AEF區域進行綠化,滿足:EF=1米,設角AEF=θ,θ ,邊界AE,AF,EF的費用為每米1萬元,區域內的費用為每平方米4 萬元.
,邊界AE,AF,EF的費用為每米1萬元,區域內的費用為每平方米4 萬元.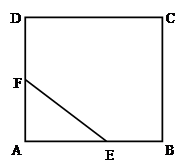
(1)求總費用y關于θ的函數.
(2)求最小的總費用和對應θ的值.
科目:高中數學 來源: 題型:解答題
某同學用“五點法”畫函數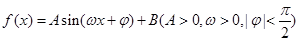 在某一
在某一
個周期內的圖象時,列表并填入的部分數據如下表:
 |  | 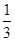 | 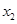 | 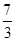 | 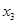 |
 |  | 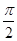 | 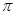 | 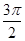 | 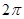 |
 |  | 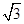 |  | 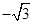 |  |
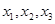 ,并直接寫出函數
,并直接寫出函數 的解析式;
的解析式; 的圖象沿
的圖象沿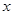 軸向右平移
軸向右平移 個單位得到函數
個單位得到函數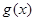 ,若函數
,若函數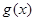 在
在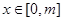 (其中
(其中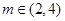 )上的值域為
)上的值域為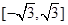 ,且此時其圖象的最高點和最低點分別為
,且此時其圖象的最高點和最低點分別為 ,求
,求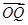 與
與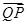 夾角
夾角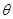 的大小.
的大小.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
已知向量 ,
, ,設函數
,設函數 ,且
,且 的圖象過點
的圖象過點 和點
和點 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)將 的圖象向左平移
的圖象向左平移 (
( )個單位后得到函數
)個單位后得到函數 的圖象.若
的圖象.若 的圖象上各最高點到點
的圖象上各最高點到點 的距離的最小值為1,求
的距離的最小值為1,求 的單調增區間.
的單調增區間.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=Acos(ωx+φ)(A>0,ω>0,- <φ<0)的圖象與y軸的交點為(0,1),它在y軸右側的第一個最高點和第一個最低點的坐標分別為(x0,2)和(x0+2π,-2).
<φ<0)的圖象與y軸的交點為(0,1),它在y軸右側的第一個最高點和第一個最低點的坐標分別為(x0,2)和(x0+2π,-2).
(1)求函數f(x)的解析式;
(2)若銳角θ滿足cosθ= ,求f(2θ)的值.
,求f(2θ)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
函數 的一段圖象過點(0,1),如圖所示.(1)求函數
的一段圖象過點(0,1),如圖所示.(1)求函數 的表達式;(2)將函數
的表達式;(2)將函數 的圖象向右平移
的圖象向右平移 個單位,得函數
個單位,得函數 的圖象,求
的圖象,求 的最大值,并求出此時自變量x的集合.
的最大值,并求出此時自變量x的集合.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,正三角形ABC的邊長為2,D,E,F分別在三邊AB,BC和CA上,且D為AB的中點, ,
,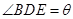 ,
,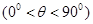 .
.
(1)當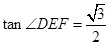 時,求
時,求 的大小;
的大小;
(2)求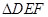 的面積S的最小值及使得S取最小值時
的面積S的最小值及使得S取最小值時 的值.
的值.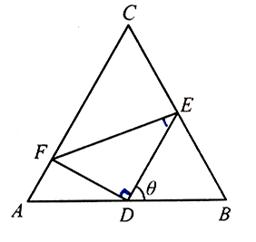
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com