
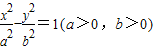 的右準線l2與一條漸近線l交于點P,F是雙曲線的右焦點.
的右準線l2與一條漸近線l交于點P,F是雙曲線的右焦點.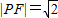 ,且雙曲線的離心率
,且雙曲線的離心率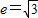 ,求該雙曲線的方程;
,求該雙曲線的方程;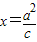 ,由對稱性,不妨設漸近線l為
,由對稱性,不妨設漸近線l為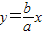 ,則
,則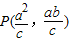 .
.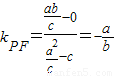 .
. ,∴
,∴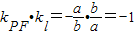 ,∴PF⊥l;
,∴PF⊥l;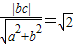 ,即b=
,即b=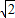 .
.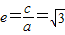 ,∴
,∴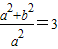 ,解得a2=1.
,解得a2=1.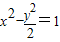 ;
;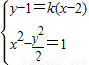 ,
,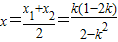 (1)
(1)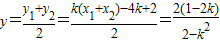 (2)
(2)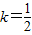 時,此時M(0,0).
時,此時M(0,0).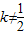 時,顯然y≠0.此時(1)÷(2)得
時,顯然y≠0.此時(1)÷(2)得 ,將其代入(2),
,將其代入(2), .∵y≠0,∴有2x2-y2-4x+y=0.顯然(0,0)也滿足此方程.
.∵y≠0,∴有2x2-y2-4x+y=0.顯然(0,0)也滿足此方程.

 口算能手系列答案
口算能手系列答案科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 3 |
| PS |
| QS |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 ,一條漸近線方程是
,一條漸近線方程是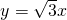 ,線段PQ是過曲線C右焦點F的一條弦,R是弦PQ的中點.
,線段PQ是過曲線C右焦點F的一條弦,R是弦PQ的中點.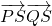 =0.當點P在曲線C上運動時,求a的取值范圍.
=0.當點P在曲線C上運動時,求a的取值范圍.查看答案和解析>>
科目:高中數學 來源:2012年廣西南寧市高三第一次適應性測試數學試卷(理科)(解析版) 題型:解答題
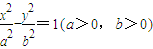 的右焦點為F,右準線為l,離心率為
的右焦點為F,右準線為l,離心率為 ,過y軸上一點A(0,b)作AM⊥l,垂足為M,則直線FM的斜率為 .
,過y軸上一點A(0,b)作AM⊥l,垂足為M,則直線FM的斜率為 .查看答案和解析>>
科目:高中數學 來源:2010年四川省資陽市高考數學三模試卷(理科)(解析版) 題型:解答題
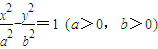 的右準線交x軸于A,虛軸的下端點為B,過雙曲線的右焦點F(c,0)作垂直于x軸的直線交雙曲線于P,過點A、B的直線與FP相交于點D,且
的右準線交x軸于A,虛軸的下端點為B,過雙曲線的右焦點F(c,0)作垂直于x軸的直線交雙曲線于P,過點A、B的直線與FP相交于點D,且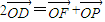 (O為坐標原點).
(O為坐標原點).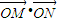 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com