
一農民有基本農田2畝,根據(jù)往年經(jīng)驗,若種水稻,則每季畝產量為400公斤;若種花生,則每季畝產量為100公斤.但水稻成本較高,每季每畝240元,而花生只需80元;且花生每公斤賣5元,稻米每公斤賣3元.現(xiàn)該農民手頭有400元,兩種作物各種多少,才能獲得最大收益?
該農民種 畝水稻,
畝水稻,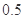 畝花生時,能獲得最大利潤,最大利潤為1650元.
畝花生時,能獲得最大利潤,最大利潤為1650元.
解析試題分析:解題思路:設量,列出限制條件不等式與目標函數(shù),作可行域,平移目標函數(shù)直線,尋找最優(yōu)解;求最優(yōu)解,回歸實際問題.規(guī)律總結:解決線性規(guī)劃應用題的步驟:(1)設有關量;(2)列出線性限制條件與目標函數(shù);(3)作可行域,平移直線找最優(yōu)解;(4)求最優(yōu)解:(5)作答.
試題解析:設該農民種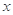 畝水稻,
畝水稻,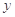 畝花生時,能獲得利潤
畝花生時,能獲得利潤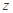 元.則
元.則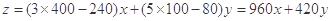 即
即
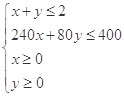 即
即 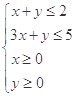
作出可行域如圖陰影部分所示, 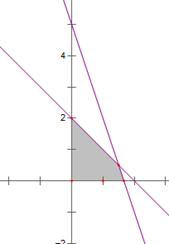
作出基準直線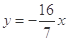 ,在可行域內平移直線
,在可行域內平移直線 ,可知當直線過點
,可知當直線過點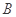 時,縱截距
時,縱截距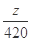 有最大值,
有最大值,
由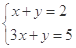 解得
解得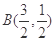 ,
,
故當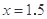 ,
,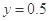 時,
時,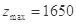 元,
元,
答:該農民種 畝水稻,
畝水稻,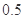 畝花生時,能獲得最大利潤,最大利潤為1650元.
畝花生時,能獲得最大利潤,最大利潤為1650元.
考點:線性規(guī)劃.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:高中數(shù)學 來源: 題型:解答題
設不等式組 表示的區(qū)域為
表示的區(qū)域為 ,不等式
,不等式 表示的平面區(qū)域為
表示的平面區(qū)域為 .
.
(1)若 與
與 有且只有一個公共點,則
有且只有一個公共點,則 =;
=;
(2)記 為
為 與
與 公共部分的面積,則函數(shù)
公共部分的面積,則函數(shù) 的取值范圍是.
的取值范圍是.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
霧霾大氣嚴重影響人們生活,某科技公司擬投資開發(fā)新型節(jié)能環(huán)保產品,策劃部制定投資計劃時,不僅要考慮可能獲得的盈利,而且還要考慮可能出現(xiàn)的虧損,經(jīng)過市場調查,公司打算投資甲、乙兩個項目,根據(jù)預測,甲、乙項目可能的最大盈利率分別為100%和60%,可能的最大虧損率分別為20%和10%,投資人計劃投資金額不超過10萬元要求確保可能的資金虧損不超過1.6萬元.
(1)若投資人用 萬元投資甲項目,
萬元投資甲項目, 萬元投資乙項目,試寫出
萬元投資乙項目,試寫出 、
、 所滿足的條件,并在直角坐標系內做出表示
所滿足的條件,并在直角坐標系內做出表示 、
、 范圍的圖形;
范圍的圖形;
(2)根據(jù)(1)的規(guī)劃,投資公司對甲、乙兩個項目投資多少萬元,才能是可能的盈利最大?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知α,β是三次函數(shù)f(x)= x3+
x3+ ax2+2bx(a,b∈R)的兩個極值點,且α∈(0,1),β∈(1,2),求動點(a,b)所在的區(qū)域面積S.
ax2+2bx(a,b∈R)的兩個極值點,且α∈(0,1),β∈(1,2),求動點(a,b)所在的區(qū)域面積S.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com