
(本小題共13分)若有窮數(shù)列{an}滿足:(1)首項a1=1,末項am=k,(2)an+1= an+1或an+1=2an ,(n=1,2,…,m-1),則稱數(shù)列{an}為k的m階數(shù)列.
(Ⅰ)請寫出一個10的6階數(shù)列;
(Ⅱ)設(shè)數(shù)列{bn}是各項為自然數(shù)的遞增數(shù)列,若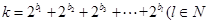 ,且
,且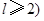 ,求m的最小值.
,求m的最小值.
(考生務(wù)必將答案答在答題卡上,在試卷上作答無效)
解:(Ⅰ)1,2,3,4,5,10或1,2,4,8,9,10. ………………2分
(Ⅱ)由已知在數(shù)列{an}中 an+1= an+1或an+1=2an,
當(dāng)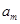 為偶數(shù)時,
為偶數(shù)時,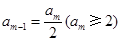 ,或
,或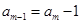 .
.
因為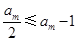
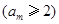 ,
,
所以在數(shù)列{an}中 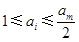 中i的個數(shù)不多于
中i的個數(shù)不多于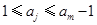 中j的個數(shù),
中j的個數(shù),
要使項數(shù)m最小,只需 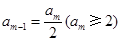 .
……………………5分
.
……………………5分
當(dāng)am為奇數(shù)時,必然有 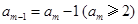 ,
,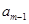 是偶數(shù),可繼續(xù)重復(fù)上面的操作.
是偶數(shù),可繼續(xù)重復(fù)上面的操作.
所以要使項數(shù)m最小,只需遇到偶數(shù)除以2,遇到奇數(shù)則減1.
因為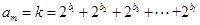 ,且
,且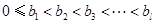 ,
,
只需除以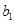 次2,得到
次2,得到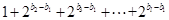 為奇數(shù);
為奇數(shù);
減1,得到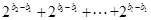 為偶數(shù),
為偶數(shù),
再除以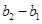 次2,得到
次2,得到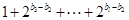 ;
;
再減1,得到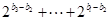 為偶數(shù),…………,
為偶數(shù),…………,
最后得到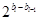 為偶數(shù),除以
為偶數(shù),除以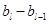 次2,得到1,即為
次2,得到1,即為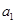 .
.
所以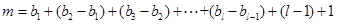 =
=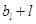 . ………13分
. ………13分
(若用其他方法解題,請酌情給分)
【解析】略



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:2011屆北京市豐臺區(qū)高三下學(xué)期統(tǒng)一練習(xí)數(shù)學(xué)理卷 題型:解答題
(本小題共13分)
已知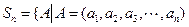 ,
,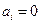 或1,
或1,
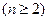 ,對于
,對于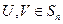 ,
,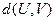 表示U和V中相對應(yīng)的元素不同的個數(shù).
表示U和V中相對應(yīng)的元素不同的個數(shù).
(Ⅰ)令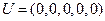 ,存在m個
,存在m個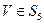 ,使得
,使得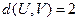 ,寫出m的值;
,寫出m的值;
(Ⅱ)令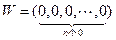 ,若
,若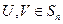 ,求證:
,求證: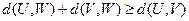 ;
;
(Ⅲ)令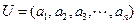 ,若
,若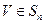 ,求所有
,求所有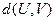 之和.
之和.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本小題共13分)
若數(shù)列![]() 滿足
滿足![]() ,則稱
,則稱![]() 為
為![]() 數(shù)列,記
數(shù)列,記![]() .
.
(Ⅰ)寫出一個E數(shù)列A5滿足![]() ;
;
(Ⅱ)若![]() ,n=2000,證明:E數(shù)列
,n=2000,證明:E數(shù)列![]() 是遞增數(shù)列的充要條件是
是遞增數(shù)列的充要條件是![]() =2011;
=2011;
(Ⅲ)在![]() 的E數(shù)列
的E數(shù)列![]() 中,求使得
中,求使得![]() =0成立得n的最小值.
=0成立得n的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本小題共13分)
若數(shù)列![]() 滿足
滿足![]() ,數(shù)列
,數(shù)列![]() 為
為![]() 數(shù)列,記
數(shù)列,記![]() =
=![]() .
.
(Ⅰ)寫出一個滿足![]() ,且
,且![]() 〉0的
〉0的![]() 數(shù)列
數(shù)列![]() ;
;
(Ⅱ)若![]() ,n=2000,證明:E數(shù)列
,n=2000,證明:E數(shù)列![]() 是遞增數(shù)列的充要條件是
是遞增數(shù)列的充要條件是![]() =2011;
=2011;
(Ⅲ)對任意給定的整數(shù)n(n≥2),是否存在首項為0的E數(shù)列![]() ,使得
,使得![]() =0?如果存在,寫出一個滿足條件的E數(shù)列
=0?如果存在,寫出一個滿足條件的E數(shù)列![]() ;如果不存在,說明理由。
;如果不存在,說明理由。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011年普通高中招生考試北京市高考文科數(shù)學(xué) 題型:解答題
本小題共13分)
若數(shù)列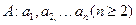 滿足
滿足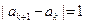
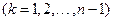 ,則稱
,則稱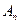 為
為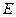 數(shù)列。記
數(shù)列。記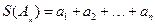 。
。
(Ⅰ)寫出一個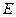 數(shù)列
數(shù)列 滿足
滿足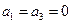 ;
;
(Ⅱ)若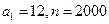 ,證明:
,證明: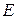 數(shù)列
數(shù)列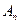 是遞增數(shù)列的充要條件是
是遞增數(shù)列的充要條件是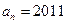 ;
;
(Ⅲ)在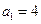 的
的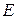 數(shù)列
數(shù)列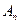 中,求使得
中,求使得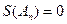 成立的
成立的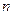 的最小值。
的最小值。
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com